Upper and lower bounds on the beta function

The beta function B(x, y) is defined by

$B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1}\, dt$

and is the normalizing constant for the beta probability distribution. It is related to the gamma function via

$B(x, y) = \frac{\Gamma(x)\,\Gamma(y)}{\Gamma(x+y)}$

The beta function comes up often in applications. It can be challenging to work with, however, and so estimates for the function are welcome.

The function 1/xy gives simple approximation and upper bound for B(x, y). Alzer [1] proved that when x > 1 and y > 1

$0 \leq \frac{1}{xy} - B(x,y) \leq b$

where the constant b is defined by

$b = \max_{x\geq1}\left( \frac{1}{x^2} - \frac{\Gamma(x)^2}{\Gamma(2x)} \right) = 0.08731\ldots$

Cerone [2] gives a different bound which varies with x and y and is usually better than Alzer’s bound. For x and y greater than 1, Cerone shows

$0 \leq \frac{1}{xy} - B(x,y) \leq C(x) C(y) \leq b'$

where

$C(x) = \frac{x-1}{x\sqrt{2x-1}}$

and

$C(x) = \frac{x-1}{x\sqrt{2x-1}}$

Cerone’s bound is slightly larger in the worst case, near x = y = (3 + √5)/2, but is smaller in general.

The difference between B(x, y) and 1/xy is largest when x or y is small. We can visualize this with the Mathematica command

    Plot3D[Beta[x, y] - 1/(x y), {x, 0.5, 2.5}, {y, 0.5, 2.5}]

which produces the following plot.

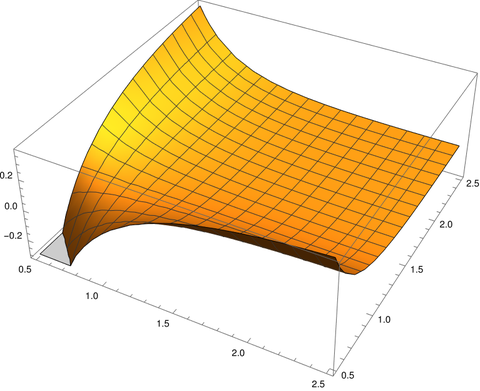
The plot dips down in the corner where x and y are near 0.5 and curls upward on the edges where one of the variables is near 0.5 and the other is not.

Let’s look at B(x, y) and 1/xy at along a diagonal slice (3t, 4t).

This suggests that approximating B(x, y) with 1/xy works best when the arguments are either small or large, with the maximum difference being when the arguments are moderate-sized. In the plot we see B(3, 4) is not particularly close to 1/12.

Next lets look at 1/xy – B(x, y) along the same diagonal slice.

This shows that the error bound C(x) C(y) is not too tight, but better than the constant bound except near the maximum of 1/xy – B(x, y).

[1] H. Alzer. Monotonicity properties of the Hurwitz zeta function. Canadian Mathematical Bulletin 48 (2005), 333–339.

[2] P. Cerone. Special functions: approximations and bounds. Applicable Analysis and Discrete Mathematics, 2007, Vol. 1, No. 1, pp. 72–91

Related posts