Swish function and a Swiss mathematician

The previous post looked at the swish function and related activation functions for deep neural networks designed to address the “dying ReLU problem.”

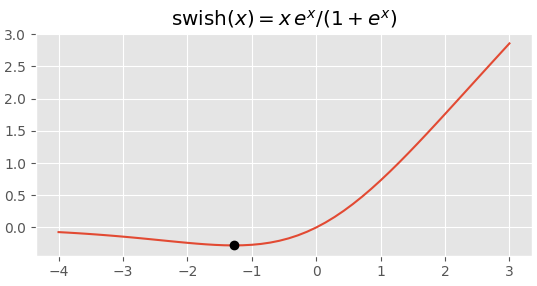
$Plot of swish(x) - \frac{ x \exp(x)}{1 + \exp(x)}$

Unlike many activation functions, the function f(x) is not monotone but has a minimum near x₀ = -1.2784. The exact location of the minimum is

$x_0 = -W\left(\frac{1}{e} \right) - 1$

where W is the Lambert W function, named after the Swiss mathematician Johann Heinrich Lambert [1].

The minimum value of f is -0.2784. I thought maybe I made a mistake, confusing x₀ and f(x₀). If you look at more decimal place, the minimum value of f is

-0.278464542761074

and occurs at

-1.278464542761074.

That can’t be a coincidence.

It turns out you can prove that f(x₀) − x₀ = 1 without explicitly finding x₀. Take the derivative of f using the quotient rule and set the numerator equal to zero. This shows that at the minimum,

$1 + x_0 + \exp(x_0) = 0$

Then

$\begin{align*} f(x_0) - x_0 &= \frac{x_0 \exp(x_0)}{1 + \exp(x_0)} - x_0 \\ &= \frac{x_0 \exp(x_0)}{1 + \exp(x_0)} - \frac{x_0 (1+\exp(x_0))}{1 + \exp(x_0)} \\ &= \frac{-x_0}{1 + \exp(x_0)} \\ &= \frac{1 + \exp(x_0)}{1 + \exp(x_0)} \\ &= 1 \end{align*}$

The fourth equation is where we use the equation satisfied at the minimum.

[1] Lambert is sometimes considered Swiss and sometimes French. The plot of land he lived on belonged to Switzerland at the time, but now belongs to France. I wanted him to be Swiss so could use “swish” and “Swiss” together in the title.

One thought on “Swish function and a Swiss mathematician”