This is the third post in a series on generalizing sine and cosine.
The previous post looked at a generalization of the sine and cosine functions that come from replacing a circle with a lemniscate, a curve that looks like a figure eight. This post looks at replacing the circle with a hyperbola.
On the unit circle, an arc of length θ starting at (1, 0) and running counterclockwise ends at (cos θ, sin θ), and this can be used to define the two trig functions. The lemniscate functions use an analogous approach, transferring arc length to a new curve.
Hyperbolic functions do not do this. Instead, they generalize a different property of the circle. Again we start out at (1, 0) and move counterclockwise around the unit circle, but this time we look at area of the sector rather than the length of the arc. The sector that ends at (cos θ, sin θ) has area θ/2. We could define sine and cosine by this relation: cos α and sin α are the x and y coordinates of where we stop when we’ve swept out an area of θ/2. This would be an awkward way to define sine and cosine, but it generalizes.
Start at (1, 0) and move along the hyperbola x² – y² = 1 in the first quadrant until the area bounded by the hyperbola, the x-axis, and a line from the origin to your location (x, y) is α/2. Then the x and y coordinates of the place where you stop are cosh x and sinh x respectively.
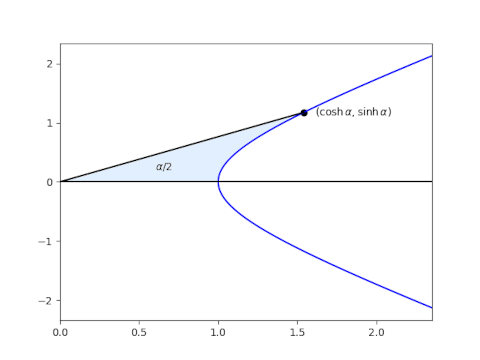
This is interesting in its own right, but it is also useful to tie together the first post in this series and the next because it is the area generalization rather than the arc length generalization that gives a geometric interpretation to the functions sinp and cosp.
