This afternoon I wrote a brief post about Terence Tao’s new paper A Maclaurin type inequality. That paper builds on two classical inequalities: Newton’s inequality and Maclaurin’s inequality. The previous post expanded a bit on Newton’s inequality. This post will do the same for Maclaurin’s inequality.
As before, let x be a list of real numbers and define Sn(x) to be the average over all products of n elements from x. Maclaurin’s inequality says that Sn(x)1/n is decreasing function of n.
S1(x) ≥ S2(x)1/2 ≥ S3(x)1/3 ≥ …
We can illustrate this using the Python code used in the previous post with a couple minor changes. We change the definition of ys to
ys = [S(xs, n)**(1/n) for n in ns]
and change the label on the vertical axis accordingly.
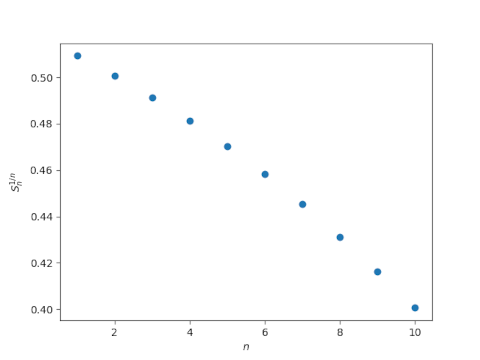
Looks like a decreasing function to me.
