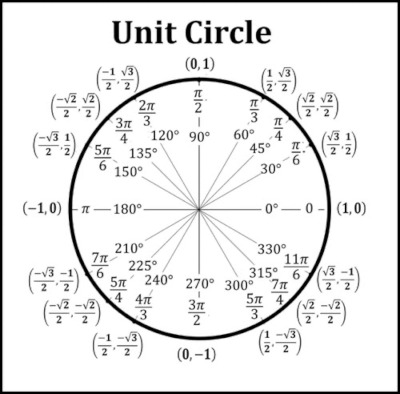
I saw a hand-drawn version of the diagram above yesterday and noticed that the points were too evenly distributed. That got me to thinking: is there any objective way to say that this famous diagram is in some sense complete? If you were to make a diagram with more points, what would they be?
Simple numbers
The numbers on the diagram are all simple. Once we’re more precise about what it means for these numbers to be “simple,” we can answer the questions above.
The angles in the diagram are all rational parts of a circle, that is, rational multiples of 2π. For the rest of the post, I’ll say “rational angle” to mean a rational multiple of 2π.
The sines and cosines all involve only one square root, i.e. no nested roots. A more useful way to express this is that all the values are the roots of a quadratic polynomial with integer coefficients.
Completeness
Could we add more rational angles whose sines and cosines are roots of quadratics? Maybe the chart would be too cluttered to put in a textbook, but would it be possible in principle? Could there be some chart analogous to the one above that has, for example, (1 + √7)/5 as one of the labels?
The angles in the common unit circle diagram, integer multiples of π/4 and π/6, are the only rational angles with sines and cosines that are roots of a quadratic polynomial with integer coefficients. That is, these are the only rational angles that have sines and cosines that are algebraic of degree 2. In that sense the diagram is complete.
The number (1 + √7)/5 is algebraic of degree 2 [1] but isn’t on our exhaustive list of possible algebraic values of degree 2. So even if you were to try numbers of the form pπ/q for very large integers p and q, you’ll never get a sine or cosine equal to (1 + √7)/5.
In 1933 Lehmer [2] showed how to classify all rational angles whose sines or cosines are algebraic of given degree. His theorem proves that the only rational angles whose sine is algebraic of degree 2 are integer multiples of π/4 and π/6.
Interestingly, there is another rational angle whose cosine is algebraic of degree 2:
cos(π/5) = (1 + √5)/4
So we could extend the unit circle diagram to include multiples of π/5, but only the cosine would be algebraic of degree 2. The sines are more complicated. For example,
sin(π/5) = √(5/8 + √(5)/8)
which is algebraic of degree 4.
Higher degrees
There are no rational angles whose sine is algebraic of degree 3, so going up to degree 3 wouldn’t help.
If we go up to degree 4 then we could add multiples of π/5, π/8, and π/12. These all have sines and cosines that are algebraic of degree 4.
Related posts
[1] (1 + √7)/5 is a root of 25x² − 10x = 6 = 0.
[2] D. H. Lehmer. A Note on Trigonometric Algebraic Numbers. The American Mathematical Monthly , March 1933, Vol. 40, No. 3, pp. 165–166
