Let ℤ² be the lattice of points in the plane with integer coordinates. You could think of these points as being the centers of the squares in a chessboard extending to infinity in every direction.
Cantor tells us that the points in ℤ² are countable. What’s more surprising is that you could count the points using a knight’s move. If you place a knight at the origin, there is a way for him to visit every point exactly once.
It’s possible to tour every point in a 5 × 5 lattice as shown below.
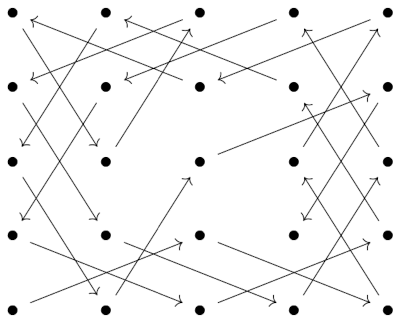
The knight’s next move would take it out of the 5 × 5 block and position it to begin touring a new 5 × 5 block bordering the first block.
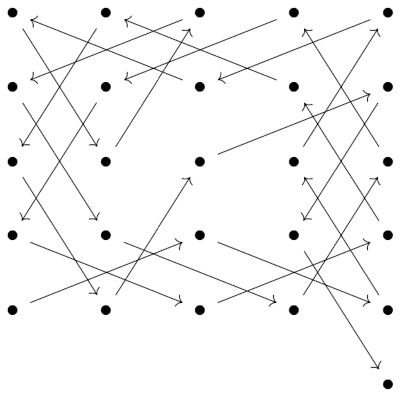
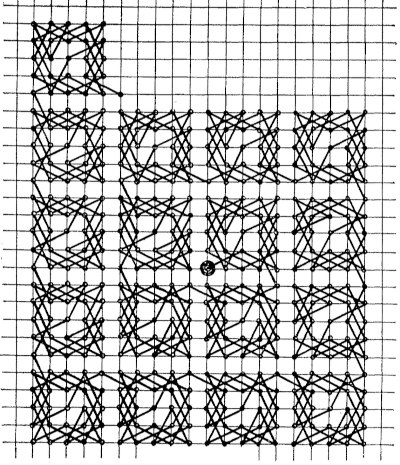
You can repeat this pattern, covering ℤ² in a spiral of 5 × 5 squares.
I produced the first two images using Quiver, an application intended for drawing commutative diagrams, though I’ve found it useful for other drawing tasks as well.
The third image was taken from a note by Robert E. Gilman on an article by Norman Anning: A Recreation. The American Mathematical Monthly, Vol. 37, No. 10 (Dec., 1930), pp. 535–538.

Distant echoes of Linguistic Geometry…. ( https://www.stilman-strategies.com/bstilman/boris_papers/Jour94_CHESS7.pdf)
LG was a tier of grammars (“language of zones, trajectories, translations”) at increasingly abstract levels of “piece moves” in order to optimize search time by reducing search tree.
Having no background in the math around grammar and languages, I found it simultaneously fascinating and impenetrable.
One of my graduate school teachers (Paul Cull) published a paper long ago showing how to walk any rectangular board ( https://www.fq.math.ca/Scanned/16-3/cull.pdf ). I like the treatment here that shows how to “diagonalize” (in a Cantor sense) outwards in a spiral.
How boring chess would be without the knight.