Barycentric coordinates are sometimes called area coordinates or areal coordinates in the context of triangle geometry. This is because the barycentric coordinates of a point P inside a triangle ABC correspond to areas of the three triangles PBC, PCA and PAB.
(This assumes ABC has unit area. Otherwise divide the area of each of the three triangles by the area of ABC. We will assume for the rest of this post that the triangle ABC has unit area.)
Areal coordinates take three numbers to describe a point in two dimensional space. Why would you do that? It’s often useful to use an overdetermined coordinate system. The benefit of adding one more coordinate is that you get a coordinate system matched to the geometry of the triangle. For example, the vertices of the triangle have coordinates (1, 0, 0), (0, 1, 0), and (0, 0, 1), regardless of the shape of the triangle.
Here is an example of a theorem [1] that is convenient to state in terms of areal coordinates but that would be more complicated in Cartesian coordinates.
First we need to define the midpoint triangle, also called the medial triangle. This is the triangle whose vertices are the midpoints of each side of ABC. In terms of areal coordinates, the vertices of this triangle are (0, ½, ½), (½, 0, ½), and (½, ½, 0).
Now let P be any point inside the midpoint triangle of ABC. Then there is a unique ellipse E inscribed in ABC and centered at P.
Let (α, β, γ) be the areal coordinates of P. Then the area of E is
Because P is inside the medial triangle, each of the areal coordinates are less than ½ and so the quantity under the square root is positive.
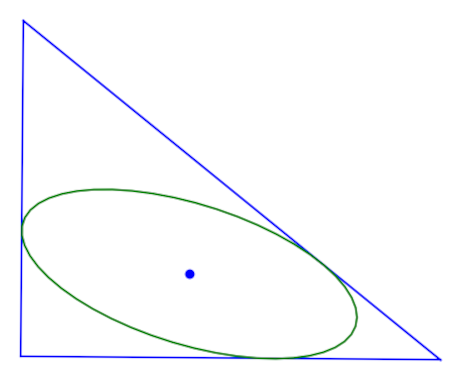
Finding the equation of the inscribed ellipse is a bit complicated, but that’s not necessary in order to find its area.
Related posts
[1] Ross Honsberger. Mathematical Plumbs. 1979
