It’s possible to place n queens on an n × n chess board so that no queen is attacking any other queen, provided n > 3. A queen is able to move any number of squares in any horizontal, vertical, or diagonal direction. Another way to put it is that the queen can move in any of 8 = 3² − 1 directions, in the direction of any cell in a 3 × 3 grid centered on the queen.
What if we extend chess to three dimensions? Now we have an n × n × n cube. Now a queen is able to move in 26 = 3³ − 1 directions, in the direction of any cell in a 3 × 3 × 3 cube centered on the queen.
Klarner [1] proved that it is possible to place n² queens in an n × n × n cube so that no queen is attacking any other, provided gcd(n, 210) = 1, i.e. provided the smallest prime factor of n is larger than 7. The condition gcd(n, 210) = 1 is sufficient, and it is conjectured to be necessary as well [2].
Klarner constructed a solution as follows: Place the queens on
(i, j, (3i + 5j) mod n)
for i and j running from 1 to n.
One way to visualize the queens in 3D is to draw a 2D grid where each cell contains the vertical coordinate of the corresponding queen. This grid will be a Latin square, and so the 3D queen placement problem is also known as the Latin queen problem.
Here’s a visualization of Klarner’s example.
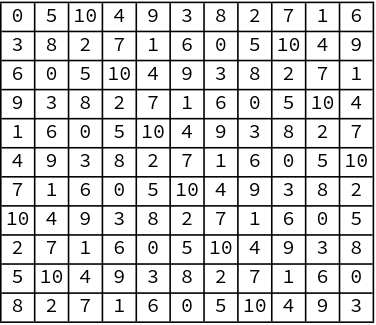
Note that if you only pay attention to a particular number, you have a solution to the 11 queens problem in a square. That’s because every slice of a 3D solution is a solution to the 2D problem.
I played around with plotting the points in three dimensions. Here’s one view.
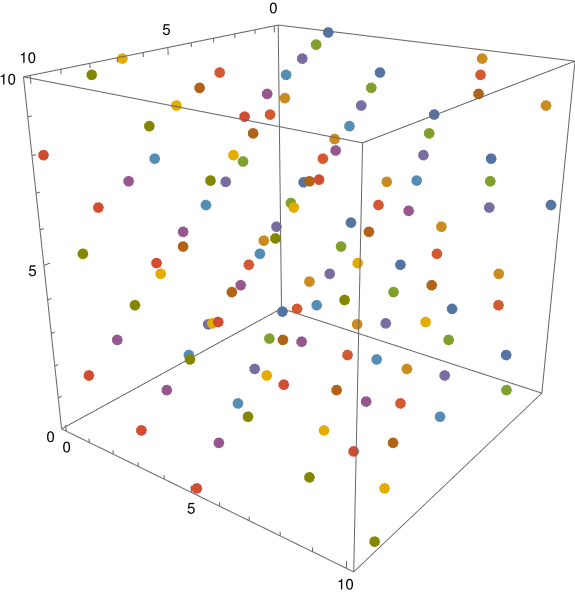
A slight rotation of the cube gives a substantially different perspective. This would be better as an animation, available here.
Mathematica code
Here’s the code that made the images above.
Flat grid:
Grid[
Table[
Mod[3 i + 5 j, 11],
{i, 0, 10},
{j, 0, 10}
],
Frame -> All
]
Static 3D view:
ListPointPlot3D[
Table[
{i, j, Mod[3 i + 5 j, 11]},
{i, 0, 10},
{j, 0, 10}
],
BoxRatios -> {1, 1, 1},
PlotStyle -> {PointSize[0.02]}
]
Animation:
Animate[
ListPointPlot3D[
Table[
{i, j, Mod[3 i + 5 j, 11]},
{i, 0, 10},
{j, 0, 10}
],
BoxRatios -> {1, 1, 1},
PlotStyle -> {PointSize[0.02]},
ViewPoint -> {2 Cos[t], 2 Sin[t], 1}
],
{t, 0, Pi, 0.05},
AnimationRunning -> True,
AnimationRate -> 4
]
Export["klerner_animation.gif", %]
Related posts
[1] D.A. Klarner, Queen squares, J. Recreational Math. 12 (3) (1979/1980) 177–178.
[2] Jordan Bell and Brett Stevens. A survey of known results and research areas for n-queens. Discrete Mathematics 309 (2009) 1–31

I had a hard time visualizing the 26 directions as being “one for each neighboring cube”, so another way to look at it is:
6 move directions for the faces of the cube (those that move on only one axis, in two directions for each axis).
12 move directions for the edges of the cube (those that move on two axes).
8 move directions for the corners of the cube (those that move on all three axes).
6+12+8=26.