Every rotation in 3D fixes an axis [1]. This is Euler’s rotation theorem from 1775. Another way to state the theorem is that no matter how you rotate a sphere about its center, two points stay fixed.
The composition of two rotations is a rotation. So the first rotation fixes some axis, the second rotation fixes some other axis, and the composition fixes some third axis. It’s easy to see what these axes are if we work with quaternions. (Quaternions were discovered decades after Euler proved his rotation theorem.)
A rotation by θ about the axis given by a unit vector v = (v1, v2, v3) corresponds to the quaternion
q = (cos(θ/2), sin(θ/2)v1, sin(θ/2)v2, sin(θ/2)v3).
To rotate a point p = (p1, p2, p3) by an angle θ about the axis v, first embed p as a quaternion by setting its first coordinate to 0:
p → (0, p1, p2, p3)
and multiply the quaternion p on the left by q and on the right by the conjugate of q, written q*. That is, the rotation takes p to
p′ = qpq*.
This gives us a quaternion p′, not a 3D vector. We recover the vector by undoing the embedding, i.e. chopping off the first coordinate.
Making things clearer
Since q has unit length, the conjugate of q is also its inverse: q* = q−1. Usually rotations are described as above: multiply on the left by q and on the right by q*. In my opinion it’s clearer to say
p′ = qpq−1.
Presumably sources say q* instead of q−1 because it’s obvious how to compute q* from q; it’s not quite as obvious that this also gives the inverse of q.
Another thing about the presentation above that, while standard, could be made clearer is the role Euclidean space and quaternions. It’s common to speak of the real and quaternion representations of a vector, but we could make this more explicit by framing this as an embedding E from ℝ³ to the quaternions ℍ and a projection P from ℍ back to ℝ³ [3].
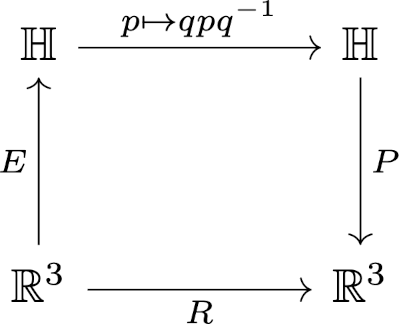
The commutative diagram says we end up with the same result regardless of which of two paths we take: we can do the rotation directly from ℝ³ to ℝ³, or we could project into ℍ, multiply by q on the left and divide by q on the right, and project back down to ℝ³.
Composition
Composing rotations represented by quaternions is simple. Rotating by a quaternions q and then by a quaterion r is the same as rotating by rq. Proof:
r(qpq−1)r−1 = (rq)p(q−1r−1) = (rq)p(rq)−1.
See the next post for how to convert between quaternion and matrix representations of a rotation.
Related posts
[1] Note that this is not the case in two dimensions, nor is it true in higher even dimensions.
[2] We assumed v had unit length as a vector in ℝ³. So
||q||² = cos²(θ/2) + sin²(θ/2) = 1.
[3] Why ℍ for quaternions? ℚ for rationals was already taken, so we use ℍ for William Rowan Hamilton.
