Given two quaternions x and y, the product xy might equal the product yx, but in general the two results are different.
How different are xy and yx on average? That is, if you selected quaternions x and y at random, how big would you expect the difference xy − yx to be? Since this difference would increase proportionately if you increased the length of x or y, we can just consider quaternions of norm 1. In other words, we’re looking at the size of xy − yx relative to the size of xy.
Here’s simulation code to explore our question.
import numpy as np
def random_unit_quaternion():
x = np.random.normal(size=4)
return x / np.linalg.norm(x)
def mult(x, y):
return np.array([
x[0]*y[0] - x[1]*y[1] - x[2]*y[2] - x[3]*y[3],
x[0]*y[1] + x[1]*y[0] + x[2]*y[3] - x[3]*y[2],
x[0]*y[2] - x[1]*y[3] + x[2]*y[0] + x[3]*y[1],
x[0]*y[3] + x[1]*y[2] - x[2]*y[1] + x[3]*y[0]
])
N = 10000
s = 0
for _ in range(N):
x = random_unit_quaternion()
y = random_unit_quaternion()
s += np.linalg.norm(mult(x, y) - mult(y, x))
print(s/N)
In this code x and y have unit length, and so xy and yx also have unit length. Geometrically, x, y, xy, and yx are points on the unit sphere in four dimensions.
When I ran the simulation above, I got a result of 1.13, meaning that on average xy and yx are further from each other than they are from the origin.
To see more than the average, here’s a histogram of ||xy − yx|| with N above increased to 100,000.
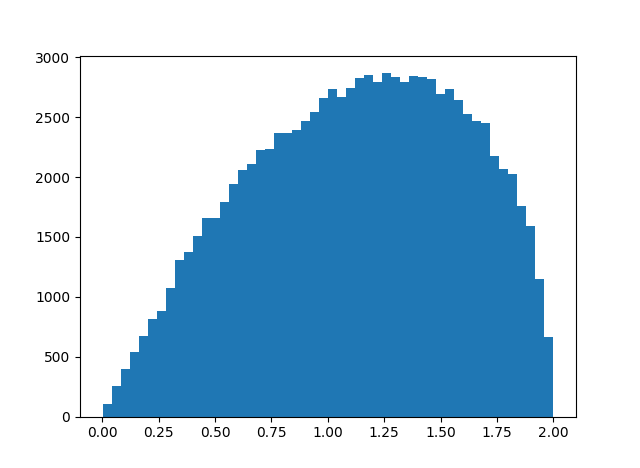
I imagine you could work out the distribution exactly, though it was quicker and easier to write a simulation. We know the distribution lives on the interval [0, 2] because xy and yx are points on the unit sphere. Looks like the distribution is skewed toward its maximum value, and so xy and yz are more likely to be nearly antipodal than nearly equal.
Update: Greg Egan worked out the exact mean and distribution.
Here’s the closed form for the distribution of |xy – yx|, the norm of the commutator between unit quaternions x, y chosen uniformly on the 3-sphere. pic.twitter.com/hoXXfQt7Zp
— Greg Egan (@gregeganSF) July 6, 2018

Hi,
Subtracting two quaternions (x-y) doesn’t make much sense to me. Normally, for subtracting quaternions (or any other member of SU group) it make more sense to multiply by their inverse (in case of quaternion, their inverse being their conjugate).
So
s += np.linalg.norm(mult(mult(x, y), -mult(y, x)))
If you run this case, the result should be 1. Which make sense, as the resulting quaternion is still member of the SU group. So I expect the result to remain on the manifold (in your case, it is not).
(I agree xy is not the same as yx, however, you can measure their different as in difference is angle/axis, not manually subtracting them)
You can simplify the commutator of two quaternions quite a bit. All terms involving a real part reduce to 0, as do all diagonal terms, leaving
[a + bi + cj + dk, A + Bi + Cj + Dk] = [bi, Cj] + [bi, Dk] + [cj, Bi] + [cj, Dk] + [dk, Bi] + [dk, Cj]
= 2bCk – 2bDj – 2cBk + 2cDi + 2dBj – 2dCi
(I’m using the shorthand [x, y] := xy – yx.) In other words, you’re discarding the first component and computing a cross product multiplied by 2.
This means that this problem is equivalent to finding the cross product of two random vectors in a 3-dimensional ball, although with a probability measure that is not uniform, but projected from a 4-dimensional sphere.
You said above: “Looks like the distribution is skewed toward its maximum value, and so xy and yz are more likely to be nearly antipodal than nearly equal.”
If you take one point as a pole, then the points on the equator are $\sqrt{2}$ units away. That means half the unit quaternions are more that $\sqrt{2}$ away.
Here is the same plot with the difference between x and y rather than between xy and yx.
http://www.nklein.com/wp-content/uploads/2018/07/S3-distance.png
The left is distance = 0, the right is distance = 2. The mode is at distance = 1.64.