Legendre polynomials

Posted on by John

The previous post mentioned Legendre polynomials. This post will give a brief introduction to these polynomials and a couple hints of how they are used in applications.

One way to define the Legendre polynomials is as follows.

  • P0(x) = 1
  • Pk are orthogonal on [−1, 1].
  • Pk(1) = 1 for all k ≥ 0.

The middle bullet point means

\int_{-1}^1 P_m(x) P_n(x) \, dx = 0

if m ≠ n. The requirement that each Pk is orthogonal to each of its predecessors determines Pk up to a constant, and the condition Pk(1) = 1 determines this constant.

Here’s a plot of the first few Legendre polynomials.

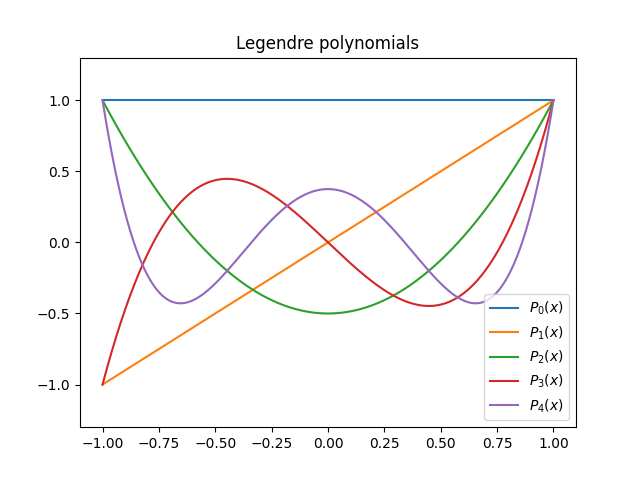
There’s an interesting pattern that appears in the white space of a graph like the one above when you plot a large number of Legendre polynomials. See this post.

The Legendre polynomial Pk(x) satisfies Legendre’s differential equation; that’s what motivated them.

(1 - x^2) y^{\prime\prime} -2x y^\prime + k(k+1)y = 0

This differential equation comes up in the context of spherical harmonics.

Next I’ll describe a geometric motivation for the Legendre polynomials. Suppose you have a triangle with one side of unit length and two longer sides of length r and y.

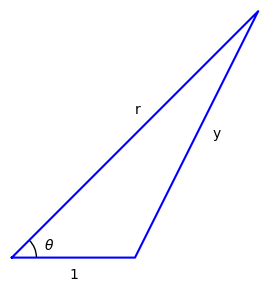
You can find y in terms of r by using the law of cosines:

y = \sqrt{1 - 2r \cos \theta + r^2}

But suppose you want to find 1/y in terms of a series in 1/r. (This may seem like an arbitrary problem, but it comes up in applications.) Then the Legendre polynomials give you the coefficients of the series.

\frac{1}{y} = \frac{P_0(\cos\theta)}{r} + \frac{P_1(\cos\theta)}{r^2} + \frac{P_2(\cos\theta)}{r^3} + \cdots

Source: Keith Oldham et al. An Atlas of Functions. 2nd edition.

Related posts

2 thoughts on “Legendre polynomials”

  2. John

    That’s interesting. I knew I typed “k” and not “\nu”. I have a script that generates the HTML and the SVG, putting the LaTeX source into the HTML alt tag. And the alt text says “k.”

    Turns out I had written about this before and had an older SVG file by the same name that used \nu.

Comments are closed.