We often want to reduce something that’s inherently two-dimensional into something one-dimensional. We want to turn graph into a list.
And we’d like to do this with some kind of faithfulness. We’d like things that are close together in 2D space to be close together in their 1D representation, and vice versa, to the extent possible.
For example, postal codes are a way of imposing a linear order on geographic regions. You would like (or maybe naively assume) that regions whose zip codes are numerically close together are geographically close together. This is roughly true. See this post to explore that further.
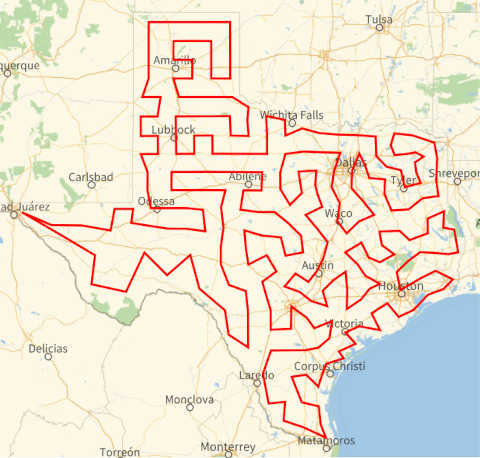
Tours are another way to turn a graph into a list. A Traveling Salesman tour is a path of shortest length through a set of points. For example, here is a Traveling Salesman tour of Texas counties. Counties that are visited consecutively are close together, though it may take a long time to come back to a county close to the one you’re in at a given time.
Sometimes there are purely mathematical reasons to flatten a 2D structure into a linear tour, such as Hilbert curves or Cantor’s diagonal trick.
All this came to mind because I saw a post on Hacker News this morning about a way to enumerate a zigzag spiral.

The remarkable thing about this article is that the author gives a sequence of closed-form expressions for the number at position (m, n) in the grid.
