A traveling salesman tour of Africa

Posted on by John

Suppose you’d like to tour Africa, visiting each country once, then returning to your starting point, minimizing the distance traveled.

Here’s my first attempt at a solution using Mathematica, based on an example in the documentation for FindShortestTour.

    africa = CountryData["Africa"]
    FindShortestTour[africa]
    GeoGraphics[{Thick, Red, GeoPath[africa[[%[[2]]]]]}]


This produced the following map:

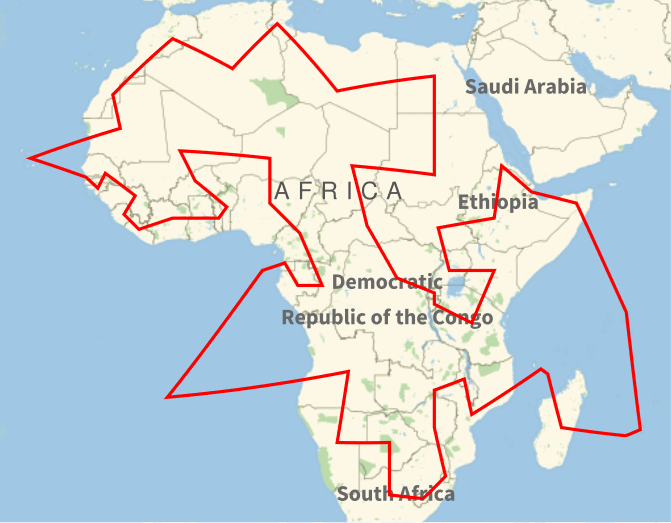
Hmm. Maybe I should have been more specific about what I mean by “Africa.” My intention was to find a tour of continental Africa, i.e. not including islands. This means I needed to remove several items from Mathematica’s list of African countries. Also, I had in mind sovereign states, not territories of overseas states and not disputed territories.

After doing this, the map is more like what I’d expect.

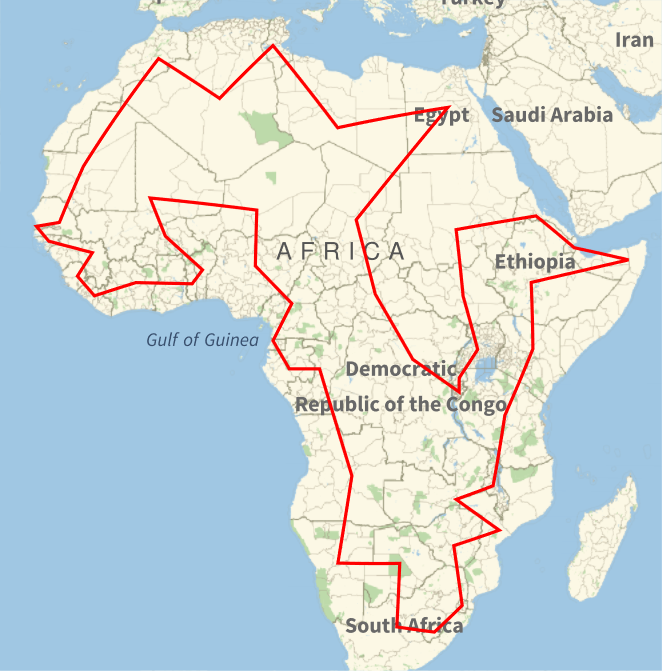
The tour is then

  1. Algeria
  2. Tunisia
  3. Libya
  4. Egypt
  5. Chad
  6. Central African Republic
  7. Democratic Republic of the Congo
  8. Burundi
  9. Rwanda
  10. Uganda
  11. South Sudan
  12. Sudan
  13. Eritrea
  14. Djibouti
  15. Somalia
  16. Ethiopia
  17. Kenya
  18. Tanzania
  19. Malawi
  20. Zambia
  21. Mozambique
  22. Zimbabwe
  23. Eswatini
  24. Lesotho
  25. South Africa
  26. Botswana
  27. Namibia
  28. Angola
  29. Republic of the Congo
  30. Gabon
  31. Equatorial Guinea
  32. Cameroon
  33. Nigeria
  34. Niger
  35. Mali
  36. Burkina Faso
  37. Benin
  38. Togo
  39. Ghana
  40. Ivory Coast
  41. Liberia
  42. Sierra Leone
  43. Guinea
  44. Guinea-Bissau
  45. Gambia
  46. Senegal
  47. Mauritania
  48. Morocco

The initial tour, including islands, foreign territories, and Western Sahara, was 23,744 miles or 38,213 kilometers. The second tour was 21,074 miles or 33915 kilometers.

Here’s a tour of just the islands, excluding foreign territories.

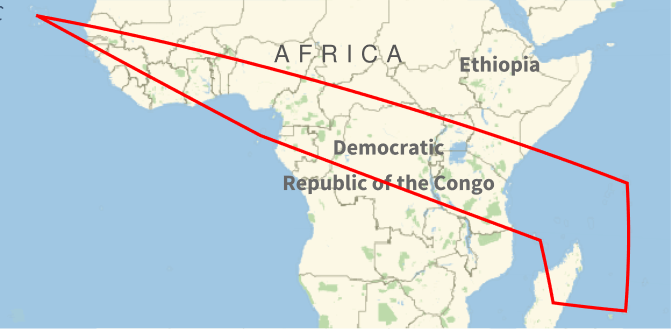
The order of the tour is

  1. Cape Verde
  2. Seychelles
  3. Mauritius
  4. Madagascar
  5. Comoros
  6. São Tomé and Príncipe

This tour is 13,034 miles or 20,976 kilometers.

Update: See the next two posts for tours of the Americas and Eurasia and Oceania.

Related posts

3 thoughts on “A traveling salesman tour of Africa”

  1. Georg Wille

    What single point is associated with each country that is then used for the tour? Is it some geometric feature (there could be problems with center of gravity or similar with concave countries) or an arbitrary point given by Mathematica?

  2. Scott

    It looks to me like John is using the center of gravity? Wouldn’t it make more sense to do a tour of the capitals? That is what I was expecting.

  3. John

    I used Mathematica’s default because that was easiest, but I could see why you might want to look at a tour of capitals instead.

    For pedagogical purposes, say memorizing a map by memorizing a tour, I think it would be better to use centers.

Comments are closed.