One common model of the hyperbolic plane is the Poincaré upper half plane ℍ. This is the set of points in the complex plane with positive imaginary part. Straight lines are either vertical, a set of points with constant imaginary part, or arcs of circles centered on the real axis. The real axis is not part of ℍ. From the perspective of hyperbolic geometry these are ideal parts, infinitely far away, and not part of the plane itself.
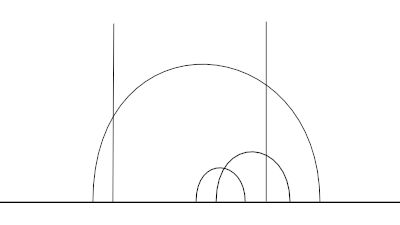
We can define a metric on ℍ as follows. To find the distance between two points u and v, draw a line between the two points, and let a and b be the ideal points at the end of the line. By a line we mean a line as defined in the geometry of ℍ, what we would see from our Euclidean perspective as a half circle or a vertical line. Then the distance between u and v is defined as the absolute value of the log of the cross ratio (u, v; a, b).
Cross ratios are unchanged by Möbius transformations, and so Möbius transformations are isometries.
Another common model of hyperbolic geometry is the Poincaré disk. We can use the same metric on the Poincaré disk because the Möbius transformation
maps the upper half plane to the unit disk. This is very similar to how the Smith chart is created by mapping a grid in the right half plane to the unit disk.