log2(3) and log2(5)

AlmostSure on X pointed out that

log₂ 3 ≈ 19/12,

an approximation that’s pretty good relative to the size of the denominator. To get an approximation that’s as accurate or better requires a larger denominator for log₂ 5.

log₂ 5 ≈ 65/28

This above observations are correct, but are they indicative of a more general pattern? Is log₂ 3 easier to approximate than log₂ 5 using rational numbers? There are theoretical ways to quantify this—irrationality measures—but they’re hard to compute.

If you look at the series of approximations for both numbers, based on continued fraction convergents, the nth convergent for log₂ 5 is more accurate than the nth convergent for log₂ 3, at least for the first 16 terms. After that I ran out of floating point precision and wasn’t sufficiently interested to resort to extended precision.

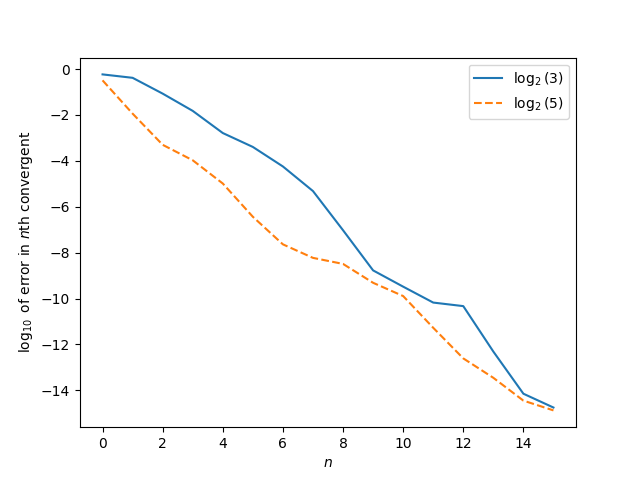
Admittedly this is a non-standard way to evaluate approximation error. Typically you look at the approximation error relative to the size of the denominator, not relative to the index of the convergents.

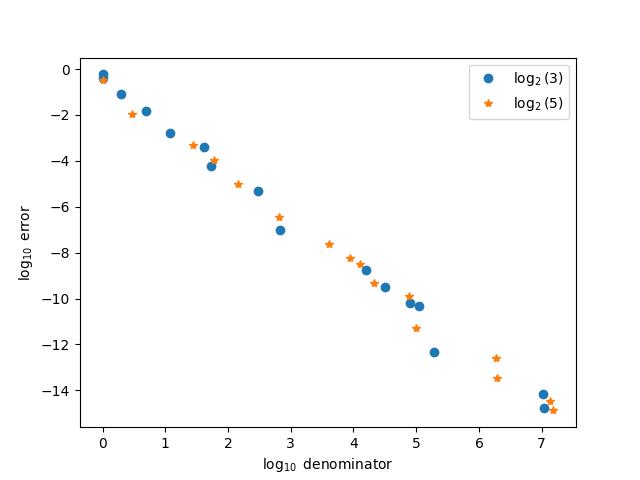
Here’s a more conventional comparison, plotting the log of approximation error against the log of the denominators.

Continued fraction posts

• Continued fractions as matrix products
• Applications of continued fractions
• Calendars and continued fractions