Let D be the unit disk in the complex plane and let f be a univalent function on D, meaning it is analytic and one-to-one on D.
There is a simple way to compute the area of f(D) from the coefficients in its power series.
If
then
The first equality follows from the change of variables theorem for functions of two variables and applying the Cauchy-Riemann equations to simplify the Jacobian. The second equality is a straight-forward calculation that you can work out in polar coordinates.
Application
Let’s apply this to what I called the minimalist Mandelbrot set the other day.
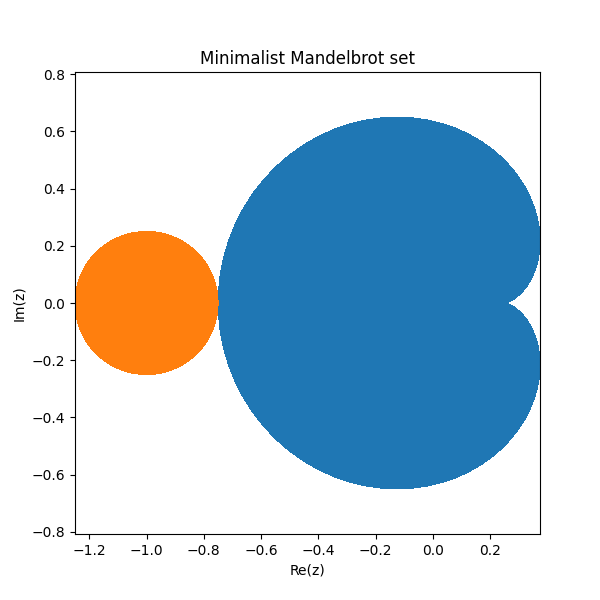
The orange disk has radius 1/4 and so its area is simply π/16.
Finding the area of the blue cardioid takes more work, but the theorem above makes it easy. The cardioid is the image of the set {α : |α| < ½} under the map f(z) = z − z². To apply the theorem above we need the domain to be the unit disk, not the unit disk times ½, so we define
as a function on the unit disk. Now c1 = ½ and c2 = −¼ and so the area of f(D) = 3π/8.
I said in the earlier post that the minimalist Mandelbrot set makes up most of the Mandelbrot set. Now we can quantify that. The area of the minimalist Mandelbrot set is 7π/16 = 1.3744. The area of the Mandelbrot set is 1.5065, so the minimalist set shown above makes up over 91% of the total area.

Ignoring the injectivity condition and applying this to f(z) = z^k gives area(f(D)) = pi * k. This could be interpreted in terms of the image of the unit disc under f covering the unit disc k times.