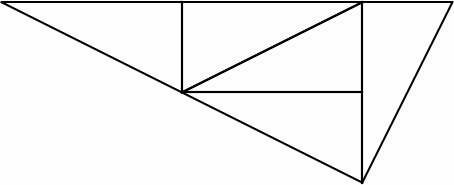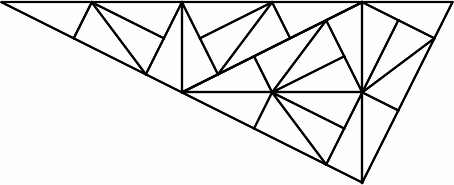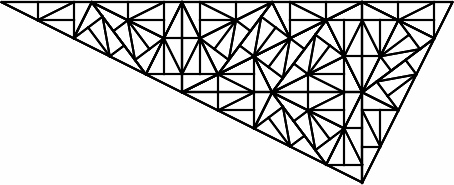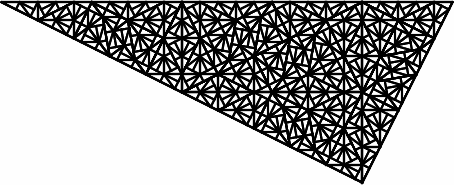
John Conway discovered a right triangle that can be partitioned into five similar triangles. The sides are in proportion 1 : 2 : √5.
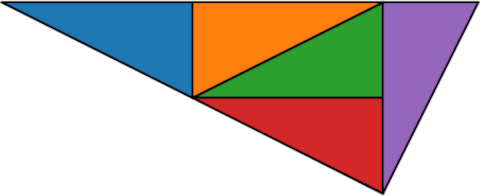
You can make a larger similar triangle by making the entire triangle the central (green) triangle of a new triangle.
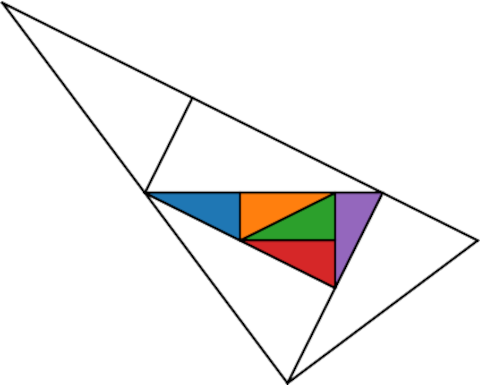
Here’s the same image with the small triangles filled in as in the original.
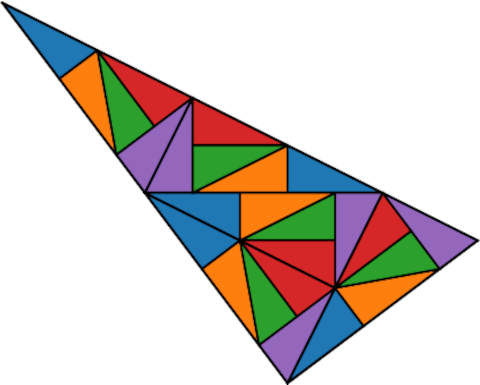
Repeating this process creates an aperiodic tiling of the plane.
The tiling was discovered by Conway, but Charles Radin was the first to describe it in a publication [1]. Radin attributes the tiling to Conway.
Alternate visualization
It would be easiest to illustrate the tiling if we were standing together in a room and placing new triangles on the floor, watching the tiling expand. Given the limitations of a screen, it may be easier to visualize subdividing the triangle rather than tiling the plane.
Imagine the smallest triangles are a constant size and at each step we’re viewing the process from further away. We see a constant size outer triangle at each step, but the triangle is growing and covering the plane.
Here’s an animated GIF of the process.
Related posts
[1] Charles Radin. “The Pinwheel Tilings of the Plane.” Annals of Mathematics, vol. 139, no. 3, 1994, pp. 661–702.

The bottom of my home page has this as a PostScript signature:
%!PS % -John Tromp http://tromp.github.io/
/t{dup 1 sub gsave dup 0 gt{[.4 .2 -.2 .4 .4 .2]concat t currentgray
.8 mul .2 add setgray -1 1 scale t -1 2 translate t 1 -1 scale t[0 1
1 0 0 2]concat t pop}{0 moveto 1 0 lineto 0 2 lineto closepath clip
fill}ifelse grestore}def 10 10 translate 600 600 scale 5 t showpage
which outputs this pinwheel tiling https://tromp.github.io/img/pinwheel.pdf