The name “complex analysis” is unfortunate. It’s called complex because it studies functions of complex numbers, which are also unfortunately named.
Complex variables, simple solutions
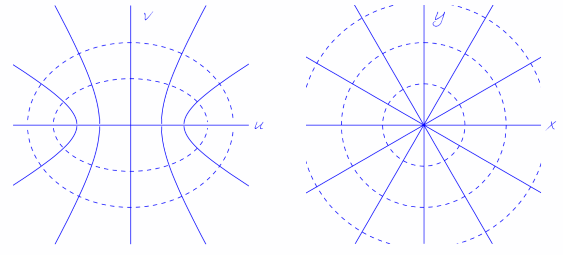
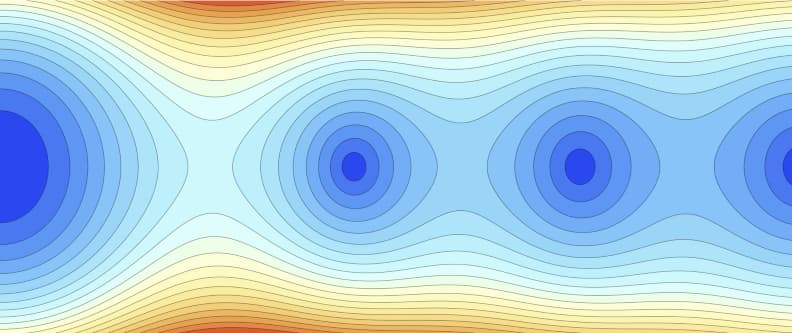
Complex numbers often simplify calculations, and functions of a complex variable have amazing properties that can greatly simplify analysis. (They can also make pretty pictures, such as the phase plot above.)
When a function of a real variable is differentiable, that tells us a few useful things about the function. But when a function of a complex variable is differentiable, that tells us an enormous amount. Because of the extra freedom of motion in two dimensions, requiring that the limit in the definition of a derivative exist is a very restrictive condition. And yet many of the functions that come up most in application satisfy this restriction: the gamma function, Bessel functions, most well-known probability distributions, etc.
“The shortest path between two truths in the real domain passes through the complex domain.” — Jacques Hadamard
Requiring that a complex function be differentiable rules out a lot of ill-behaved functions and leaves well-behaved functions that we care about in application. A function is called analytic where it is differentiable. If it’s differentiable everywhere in the complex plane, it’s called entire, which is even more restrictive and tells us even more. Usually we’re interested in functions that are analytic but with some restrictions. These functions are sometimes called holomorphic or meromorphic. Knowing that a function is analytic, even in a small neighborhood, tells us that it is infinitely differentiable, it has a power series, it cannot have local maxima or minima, it satisfies a mean value theorem, it is uniquely determined by its values on any set of points with a limit point, etc.
Applications of complex analysis
Because complex functions have such incredible properties, they are useful even for problems that at first don’t seem to involve complex numbers. Far from wanting to avoid complex functions because they are “complex,” applied mathematicians look for ways to introduce complex functions because they simplify analysis.
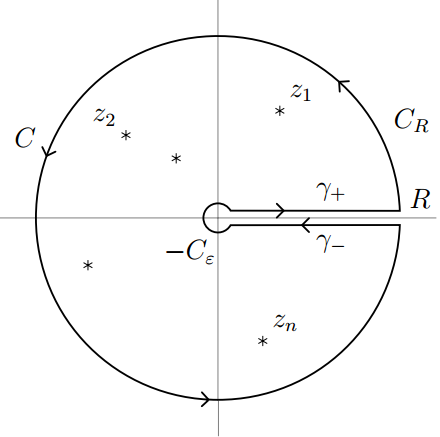
Contour integration
The best known example of this is contour integration. The integral of a complex function along a closed path doesn’t depend on the path itself but on certain values (“residues”) associated with places inside the path where the function has a singularity. This means that it is often easier to integrate a real function of a real variable by converting it into a problem involving a contour integral in the complex plane.
Design and control
Electrical circuits with alternating current are one of the first places engineers see complex variables. Digital filters are designed by looking the locations of zeros and poles in the complex plane. You can tell a lot about the behavior of a filter from where the zeros and poles of its z-transform lie.
With control theory you don’t just passively observe where zeros and poles lie but actively design systems to have zeros and poles in favorable locations.
Generating functions
Another example of where people simplify a problem by introducing complex functions is generating functions. In calculus, you might have a homework problem to find the power series coefficients of a function. Generating functions turn this on its head, taking a sequence of numbers and making them the power series coefficients of a function. (Electrical engineers do the same thing in signal processing, but they talk about z-transforms rather than generating functions, though they’re essentially the same thing.) Generating functions make discrete problems easier by turning them into continuous problems. Complex analysis techniques applied to these generating functions can squeeze out additional information, such as asymptotic bounds on the coefficients of the series.
Fourier analysis
Fourier series and Fourier transforms are defined in terms of complex analysis, and Fourier analysis comes up everywhere: in probability, signal processing, differential equations, etc. The generating functions and z-transforms mentioned above are closely related to Fourier transforms.
Laplace transforms are a variation on Fourier transforms. Undergraduate classes prefer Laplace transforms to Fourier transforms because they (appear to) avoid complex variables. But the inverse of a Laplace transform requires complex analysis.
Conformal mapping
Another common application of complex analysis is conformal mapping, using the magical properties of analytic functions to map a region of one shape into a region of another shape in a way that has lots of nice mathematical properties. You might, for example, want to transform a mechanical problem on a complicated domain into an equivalent problem on a circular disk. You might focus on a disk where things are easier to visualize and understand, then invert a conformal mapping to translate your findings back to the original domain.
Eigenvalues
Eigenvalues are one of the most common ways complex numbers appear somewhat unexpectedly. Everything can be described by real numbers, but then complex numbers pop out once you compute eigenvalues. And these eigenvalues can be very informative. For example, in a differential equation describing a mechanical system, complex eigenvalues tell you something is oscillating. If these eigenvalues have negative real parts, the oscillations will decay over time.
Help applying complex analysis
If you’d like help using the power of complex analysis to simplify your work, please call or email to discuss your project.
Trusted consultants to some of the world’s leading companies