Here’s something surprising: You can apply a symmetric function to a symmetric shape and get something out that is not symmetric.
Let f(z) be the average of z and its reciprocal:
f(z) = (z + 1/z)/2.
This function is symmetric in that it sends z and 1/z to the same value.
Now apply f to circles in the complex plane, varying the center and the radius. Here are some examples of what the image of circles are.
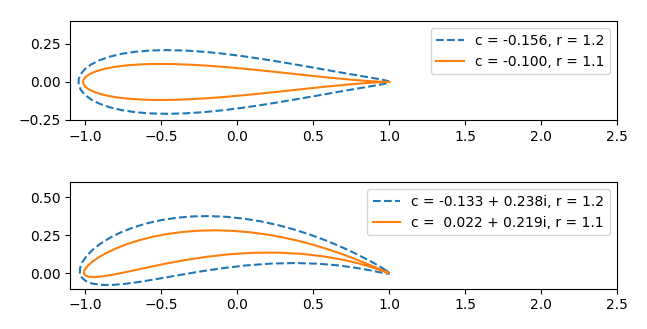
These shapes look a lot like a cross section of an airplane wing, i.e.an airfoil. You can vary the radius of the circle to change the thickness of the airfoil and you can vary the imaginary part of the center to control the camber, how much the center of the airfoil bends [1].
The reason the symmetric function f applied to a symmetric shape can give a non-symmetric shape is that the word “symmetric” is being used in different senses. Still, it is surprising to see a complicated shape pop out of a simple function applied to a simple shape. Also, although the circle is perfectly smooth, the image of the circle has a sharp cusp. This is because the circles include or approach the singularity of f at 0.
The function f above is called the Joukowsky transformation, named after Nicolai Joukowsky (Никола́й Жуко́вский) who published its application to airfoils in 1910. The Joukowsky transformation gives a conformal map between a disk and an airfoil. This map lets engineers map problems from the difficult geometry of an airfoil to the simple geometry of a disk, and then map back to the airfoil. You could design an airfoil to have the shape of the transformation of a circle, or you could design a transformation so that the image of a circle approximates your airfoil.
The function f doesn’t map every circle to an airfoil-like shape, though of course aerospace engineers are most interested in the case where you do. Also, in the examples above the trailing edge of the airfoil comes to a cusp. This is not always the case; you can adjust the circle so that you have a more rounded trailing edge. The following plot illustrates both these possibilities.
More conformal mapping posts
[1] The thickness of the airfoil doesn’t depend on the radius R so much as the ratio R/a where the circle has center
c = a – R exp(-iβ).
The ratio R/a is related to the thickness, and the parameter β is related to the camber.

Dear John,
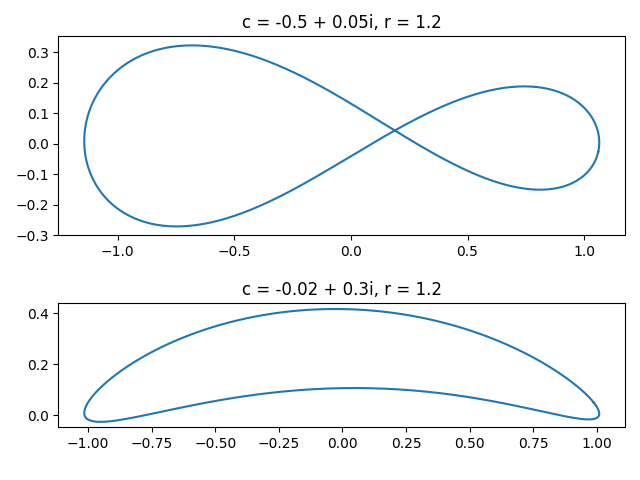
I am interested in the airfoil mapping you describe, but I am unable to reproduce any of the plots you show. I can’t see where I have gone wrong. I include a short Python program which I believe follows your final example, but only produces a sort of squashed circle, and not the airfoil shape.
import matplotlib.pyplot as plt
import numpy as np
n = 101
c = -0.02 + 0.3j
r = 1.2
theta = np.linspace ( 0.0, 2.0 * np.pi, n )
z = r * ( np.cos ( theta ) + np.sin ( theta ) * 1j )
fz = 0.5 * ( z + 1.0 / z )
plt.plot ( np.real ( fz ), np.imag ( z ), ‘b.’ )
plt.axis ( ‘equal’ )
plt.show ( )
You need to shift your circle by c.