Textbooks often present the normal approximation to the binomial, the normal approximation to the Poisson, and the Poisson approximation to the binomial. Is this last approximation redundant? Are the binomial and the Poisson close because they’re both close to the normal, or are they closer to each other than either is to the normal?
The normal approximation to the binomial works best when n is large. That is, the distribution of a binomial(n, p) random variable is close to the distribution of a normal random variable with mean np and variance np(1-p) when np is “large.” (See these notes for more detail on what “large” means.)
The normal approximation to the Poisson works best when λ is large. That is, the distribution of a Poisson(λ) random variable is close to that of a normal random variable with mean λ and variance λ. (See these notes for details.)
The direct approximation of the binomial by the Poisson says that a binomial(n,p) random variable has approximately the same distribution as a Poisson(np) random variable when np is large. This is not surprising because when np is large, both the binomial and Poisson distributions are well approximated by a normal distribution. Two things close to the same thing are close to each other. (Well, not quite the same thing. See note below.) But conceivably the Poisson and binomial distributions could be even closer to each other than they are to their normal approximations. However, it looks like this is not the case.
The following graph shows the PMF of a Poisson(10) distribution minus the PMF of a binomial(20,0.2) distribution.
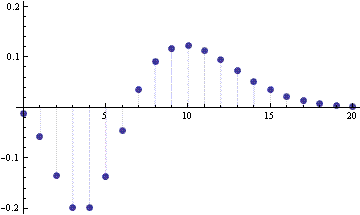
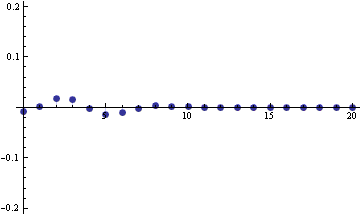
The graph below shows the difference between the PMF of a binomial(20,0.2) distribution and its normal approximation on the same vertical scale as the graph above.
Here’s the normal approximation to the Poisson(10) PMF.
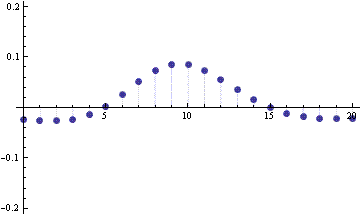
So at least in this example, binomial distribution is quite a bit closer to its normal approximation than the Poisson is to its normal approximation.
NB: the normal approximations to the binomial(n, p) and a Poisson(np) distributions are not quite the same. Both normal approximations have mean np, but the former has variance np(1-p) while the latter has variance np.
From the triangle inequality, we have
|Poisson – binomial| ≤ |Poisson – Poisson approx| + |Poisson approx – binomial approx| + |binomial approx – binomial|.
In this example, the largest term on the right is the difference between the normal approximations to the binomial and the Poisson. In fact,
|Poisson – binomial| ≈ |Poisson approx – binomial approx|.
Other approximations
See also notes on the normal approximation to the beta, binomial, gamma, Poisson, and student-t distributions.
