Design theory

How many Latin squares are there?

Posted on by John

12345, 21534, 34251, 45123, 53412

A Latin square is an n × n grid with a number from 1 to n in each cell, such that no number appears twice in a row or twice in a column.

It’s not obvious that Latin squares exist for all n, but they do, and in fact there are a lot of them. The exact number is known only for n ≤ 11. See [1] for the known values. There are upper and lower bounds for all n, and this post will look at how good the bounds are.

A particularly simple result is that number of Latin squares of size n is bounded below by the superfactorial of n [2]. That is, if Ln is the number of Latin squares of size n and the superfactorial of n is defined by

S(n) = 1! × 2! × 3! × … × n!

then

Ln ≥ S(n).

A reduced Latin square is a Latin square in which the elements of the first row and first column are in numerical order. The image at the top of the post is a reduced Latin square. If Rn is the number of reduced Latin squares of size n then

Ln = n! (n − 1)! Rn

and so we can divide the lower bound on Sn by n! (n − 1)! to get a lower bound on Rn:

Rn ≥ S(n − 2).

Ronald Alter [2] gives the following upper bound on Rn:

R_n \leq \prod_{k=1}^{n-1} (n-k)^{k-1}(n-k)!

Here’s now the lower bound, exact value, and upper bound compare for n up to 6.

    |---+-------+-------+---------|
    | n | lower | exact |   upper |
    |---+-------+-------+---------|
    | 1 |     1 |     1 |       1 |
    | 2 |     1 |     1 |       1 |
    | 3 |     1 |     1 |       2 |
    | 4 |     2 |     4 |      24 |
    | 5 |    12 |    56 |    3456 |
    | 6 |   288 |  9408 | 9553280 |
    |---+-------+-------+---------|

The numbers get very big for larger n. so let’s switch over to a log scale.

Here’s a plot corresponding to the logarithms of the values above, including all known values of Rn.

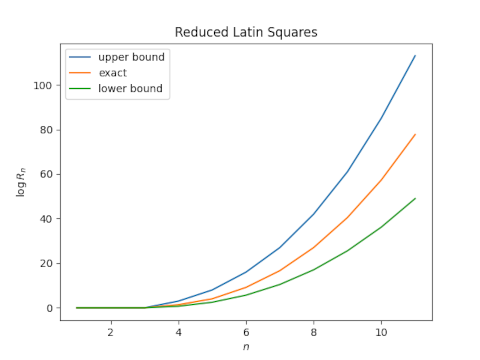
The lower and upper bounds are remarkably symmetric about the exact value, which suggests that their average would make a good estimate. Let’s look at a plot.

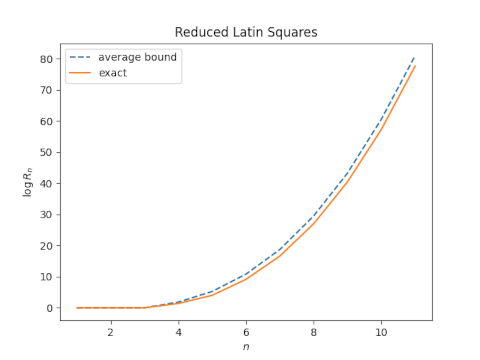Indeed, the average of the logs of the bounds is very close to the log of the actual value. This says the number of reduced Latin squares of size n is approximately the geometric mean of its upper and lower bounds, at least for n up to 11.

We can factor S(n-2) out of the upper bound on Rn when computing the geometric mean, and this gives us the approximation

R_n \approx S(n-2)\sqrt{(n-1)!} \,\,\prod_{k=1}^{n-1} (n-k)^{(k-1)/2}

References

[1] OEIS A000315

[2] Ronald Alter. The American Mathematical Monthly. Vol. 82, No. 6 (Jun. – Jul., 1975), pp. 632-634