Say you have a function f(x) and you want to find a polynomial p(x) that agrees with f(x) at several points. Given a set of points x₀, x₁, x₂, … x_n you can always find a polynomial of degree n such that p(x_i) = f(x_i) for i = 0, 1, 2, …, n. It seems reasonable that the more points you pick, the better the interpolating polynomial p(x) will match the function f(x). If the two functions match exactly at a lot of points, they should match well everywhere. Sometimes that’s true and sometimes it’s not.

Here is a famous example due to Carle Runge. Let f(x) = 1/(1 + x²) and let p_n be the polynomial that interpolates f(x) at n+1 evenly spaced nodes in the interval [-5, 5]. As n becomes larger, the fit becomes worse.

Here’s a graph of f(x) and p₉(x). The smooth blue line is f(x) and the wiggly red line is p₉(x).

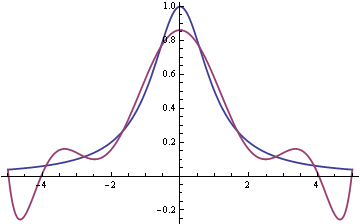
Here’s the analogous graph for p₁₆(x).

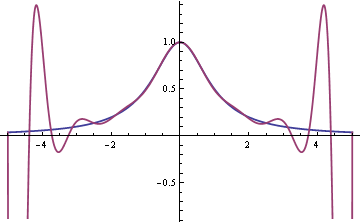
The fit is improving in the middle. In fact, the curves agree to within the thickness of the plot line from say -1 to 1. But the fit is so bad in the tails that the graph had to be cut off. Here’s another plot of f(x) and p₁₆(x) on a different scale to show how far negative the polynomial dips.

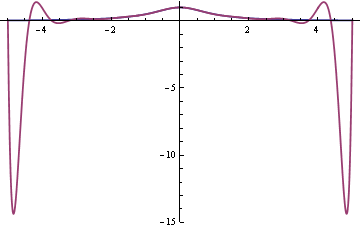
The problem is the spacing of the nodes. Interpolation errors are bad for evenly spaced nodes.

Update: This post explains in a little more depth why this particular function has problems and gives another example where interpolation at evenly-spaced nodes behaves badly.

If we interpolate f(x) at different points, at the Chebyshev nodes, then the fit is good.

The Chebyshev nodes on [-1, 1] are x_i = cos( π i / n ). Here we multiplied these nodes by 5 to scale to the interval [-5, 5].

If the function f(x) is absolutely continuous, as in our example, then the interpolating polynomials converge uniformly when you interpolate at Chebyshev nodes. However, ordinary continuity is not enough. Given any sequence of nodes, there exists a continuous function such that the polynomial interpolation error grows like log(n) as the number of nodes n increases.

Some numerical integration methods are based on interpolating polynomials: fit a polynomial to the integrand, then integrate the polynomial exactly to approximate the original integral. The examples above suggest that increasing the order of such integration methods might not improve accuracy and might even make things worse.

Related: Need help with interpolation?