Johann Kepler discovered in 1596 that the ratios of the orbits of the six planets known in his day were the same as the ratios between nested Platonic solids. Kepler was understandably quite impressed with this discovery and called it the Mysterium Cosmographicum.
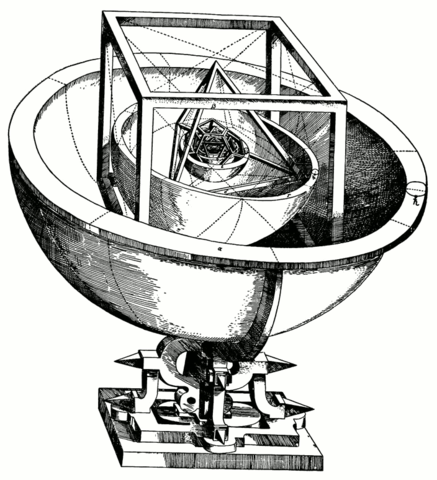
I heard of this in a course in the history of astronomy long ago, and have had in the back of my mind that one day I’d look into this in detail. How exactly do you fit these regular solids together? How well do the planetary ratios match the regular solid ratios?
Imagine the orbit of each planet being the equator of a spherical shell centered at the sun. The five regular solids fit snugly into the spaces between the shells. Between Mercury and Venus you can insert an octahedron. Its inradius is the distance of Mercury to the sun, and its circumradius is the distance of Venus to the sun. You can fit the other regular solids in similarly, the icosahedron between Venus and Earth, the dodecahedron between Earth and Mars, the tetrahedron between Mars and Jupiter, and the hexahedron (cube) between Jupiter and Saturn.
Here’s the data on the inradius and circumradius of each regular solid taken from Mathworld.
|--------------+--------------+----------|
| solid | circumradius | inradius |
|--------------+--------------+----------|
| octahedron | 0.70722 | 0.40825 |
| icosahedron | 0.95106 | 0.75576 |
| dodecahedron | 1.40126 | 1.11352 |
| tetrahedron | 0.61237 | 0.20412 |
| hexahedron | 0.86603 | 0.50000 |
|--------------+--------------+----------|
Here’s the data on average orbit radii measured in astronomical units taken from WolframAlpha.
|---------+----------|
| Planet | Distance |
|---------+----------|
| Mercury | 0.39528 |
| Venus | 0.72335 |
| Earth | 1.00000 |
| Mars | 1.53031 |
| Jupiter | 5.20946 |
| Saturn | 9.55105 |
|---------+----------|
So how well does Kepler’s pattern hold? In the table below, “Planet ratio” is the radius ratios of Venus to Mercury, Earth to Venus, etc. “Solid ratio” is the circumradius to inradius ratio of the regular solids in the order given above.
|--------------+-------------|
| Planet ratio | Solid ratio |
|--------------+-------------|
| 1.82997 | 1.73205 |
| 1.38246 | 1.25841 |
| 1.53031 | 1.25841 |
| 3.40419 | 3.00000 |
| 1.83340 | 1.73205 |
|--------------+-------------|
Not a bad fit, but not great either. I’ve heard that the fit was better given the data available to Kepler at the time; if Kepler had had more accurate data, he might not have come up with his Mysterium Cosmographicum.
By the way, notice some repetition in the solid ratios. The implied equalities are exact. The icosahedron and dodecahedron have the same ratio of circumradius to inradius because they are dual polyhedra. The same is true for the cube and the octahedron. Also, the ratio of 3 for the tetrahedron is exact.
Update: What if Kepler had known about more planets? The next planet ratios in our table above would be 2.01, 1.57, and 1.35. None of these is close to any of the solid ratios.
