The gamma function Γ(x) is the most important function not on a calculator. It comes up constantly in math. In some areas, such as probability and statistics, you will see the gamma function more often than other functions that are on a typical calculator, such as trig functions.
The gamma function extends the factorial function to real numbers. Since factorial is only defined on non-negative integers, there are many ways you could define factorial that would agree on the integers and disagree elsewhere. But everyone agrees that the gamma function is “the” way to extend factorial. Actually, the gamma function Γ(x) does not extend factorial, but Γ(x+1) does. Shifting the definition over by one makes some equations simpler, and that’s the definition that has caught on.
In a sense, Γ(x+1) is the unique way to generalize factorial. Harald Bohr and Johannes Mollerup proved that it is the only log-convex function that agrees with factorial on the non-negative integers. That’s somewhat satisfying, except why should we look for log-convex functions? Log-convexity is very useful property to have, and a natural one for a function generalizing the factorial.
Here’s a plot of the logarithms of the first few factorial values.
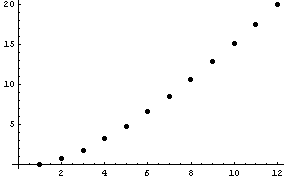 The points nearly fall on a straight line, but if you look closely, the points bend upward slightly. If you have trouble seeing this, imagine a line connecting the first and last dot. This line would lie above the dots in between. This suggests that a function whose graph passes through all the dots should be convex.
The points nearly fall on a straight line, but if you look closely, the points bend upward slightly. If you have trouble seeing this, imagine a line connecting the first and last dot. This line would lie above the dots in between. This suggests that a function whose graph passes through all the dots should be convex.
Here’s what a graph showing what the gamma function looks like over the real line.
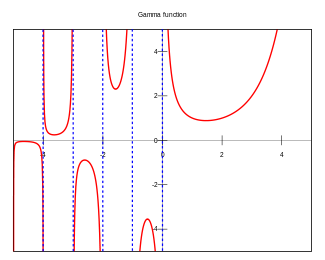
The gamma function is finite except for non-positive integers. It goes to +∞ at zero and negative even integers and to -∞ at negative odd integers. The gamma function can also be uniquely extended to an analytic function on the complex plane. The only singularities are the poles on the real axis.

John,
You’ve truly entered the realm of chart porn:
The first graph is what every VP of marketing dreams of when launching a new product.
The second graph looks like something one would use while designing an automated milking machine for cows.
The third graph… No comment.
In all seriousness, great posting. I cannot tell you how often I ran into the gamma function in statistical thermo class back in 1972… *sigh*
Nice post, John.
The second graph is like a secant (or cosecant) curve badly drawn by a student…
Being Australian, I love the name of your blog – and noted your correct spelling :-)
The gamma function does appear on some calculators. I use hp calculators and they implement the factorial function x! as gamma(x+1).
Hi John
Mind if I ask what software you used to generate the third graph please?
Cheers,
Mike
Mike,
I only made the first graph; I linked to the other two from Wikipedia. I imagine you could make this sort of graph with Mathematica. I’ve seen Mathematica plots of complex functions that use height to indicate absolute value and use color to indicate phase.
An Interesting property of the gamma function:
If you define P(x) = ∫ Γ(x) dx, then
P(x+1) = ∫ xΓ(x) dx
Integration by parts gives
∫ P(x) dx = xP(x) – P(x+1)
Since the integral of P(x) is polynomial in P(x), all succeeding integrals are also. It gets a little messier when converting to the definite integral.
This also works for Q(x) defined as
Q(x) = ∫ dx/Γ(x+1)
Integration by parts results in
∫Q(x) dx = xQ(x) – Q(x-1)
which, of course, is polynomial in all succeeding integrals also. In this case, the definite integral is straightforward.
> plot( factorial, 1, 100, log = "y", lwd = 3, col = "#444444", las=1, main = "Gamma function vs y=x", ylab="", xlab="" )> abline(a=0, b=1, col = "red", lwd=2 )
http://imgur.com/1ZglP
“at are”
Actually I’m not sure that’s true. I saw this discussion on reddit “Is the gamma function mis-defined?, or Hadamard versus Euler: Who found the better gamma function?” the article is here: http://www.luschny.de/math/factorial/hadamard/HadamardsGammaFunction.html
Hello Sir,
Why does the gamma function use in probability and Statistics? And why it is employed in some statistical distribution especially in Studentized range distribution? Thankyou sir for your response.
One way the gamma function comes up in probability and statistics is it’s association with the normal distribution. When you have a multivariate normal distribution in polar coordinates, the gamma function pops up in the density in the radial direction. (More details here.)
You may have heard of the chi-squared distribution. It’s a special case of the gamma distribution, whose PDF is the integrand defining the gamma function.
The gamma function also pops out of working with beta distributions. The normalizing factor in beta distributions is the product of two gamma function values divided by another gamma function value.