How do you quantify how loud a sound is? Sounds like a simple question, but it’s not.
What is loudness?
It’s not hard to measure the physical intensity of a sound, but loudness is the perceived intensity of a sound. It is not a physical phenomena but a psychological phenomena.
Loudness is subjective, but not entirely so. There is general consensus regarding what it means for two sounds to be equally loud, and even for ratios, such as saying when one sound is twice as loud as the other. Loudness is quantifiable, but not easily so.
What does loudness depend on?
Loudness depends on several properties of a sound, such as its frequency, bandwidth, and duration. Loudness must depend on frequency because sounds that are too low or too high have no loudness at all because we simply cannot hear them. But even with the range of audible frequencies, loudness varies quite a bit by pitch. The graph below, via Wikipedia, shows equal loudness contours. The blue lines are from work by Fletcher and Munson in 1937. The red lines are the revised curves per the ISO 226:2003 standard.
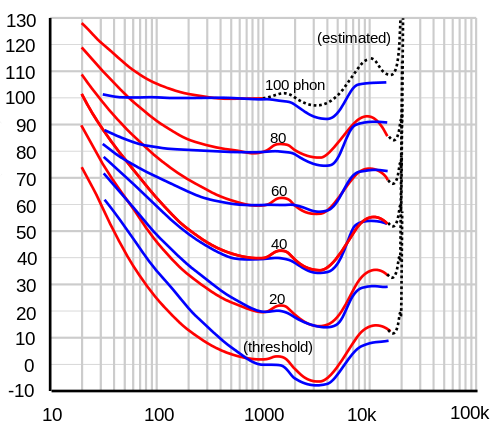
The horizontal axis is frequency in Hz and the vertical axis is sound pressure level in decibels. The contour lines represent combinations of frequency and sound pressure level that are perceived to be equally loud. If a tuba and a flute sound equally loud, the sound pressure level coming from the tuba is much higher.
Notice that the curves are not parallel, They’re much closer together for low frequencies than for midrange frequencies, though they are roughly parallel for high frequencies. This means that if you recorded a piano, for example, playing each of its keys at equal loudness, the pitches wouldn’t sound equally loud unless you played the recording back at its original volume.
Complexities and simplifications
As complicated as this is, it’s still a simplification. It is based on pure tones, simple sine waves. A single musical instrument, much less an orchestra or a jackhammer, are more complicated. Loudness is highly nonlinear, and so you cannot say that the loudness of two sounds is the sum of their individual loudnesses. A-weighting is a relatively simple way to convert sound pressure levels to loudness, but is only accurate for pure tones at fairly low loudness levels.
To simplify thing further, consider a single pure tone, a sine wave at 1 kHz. (This is almost two octaves above middle C. See details here.) Loudness level in phons is defined to match sound pressure level in decibels for a 1 kHz pure tone. So a sound has a loudness level of 40 phons, for example, if it is perceived to be as loud as a pure 1 hKz tone at 40 dB.
At 1 kHz, loudness increases by a factor of 2 for every 10 dB increase in sound pressure level. But because nothing is simple in psychoacoustics, even this is a simplification. It only holds for sounds with loudness level 40 dB or greater. A quiet room is around 40 phons, so the added complications below 40 phons may not be relevant in many applications.
A pure tone at 1 kHz and 20 dB sounds more than four times softer than the same tone at 40 dB. The definition of loudness level in phons still holds below 40 phons. An oboe has a loudness level of 20 phons if it has the same loudness as a sine wave with frequency 1 kHz and sound pressure level 20 dB. But an oboe at 30 phons will sound more than twice as loud as one at 20 phons.
Update: New blog post comparing guitar samples at the same sound pressure level but with differing loudness and sharpness.
Summary
So where are we as far as calculating loudness? We’ve said a lot about what you can’t do, what complications have to be considered. But we’ve concluded this much: for a pure 1 kHz tone, the loudness in phons equals (by definition) the sound pressure level in decibels. And we’ve said how in principle you could define the loudness of other sounds: compare them to a 1 kHz tone that’s just as loud. We haven’t said how to compute this, only how you could determine it empirically.
In future posts I may write about how you do this using the ISO 532B standard or the newer ANSI S3.4-2007 standard.

“At 1 kHz, loudness increases by a factor of 2 for every 10 dB increase in sound pressure level.”
I’m a bit confused: A 10dB increases power by a factor of 10, right? And (at 1kHz) increases loudness (as measured in phons) by 10 phons? But it doubles the loudness?
I had thought the reason for the dB log scale (by phons, by extension) is that perception of loudness is roughly logarithmic in power: each 10dB increase increases power by 10x, but (very roughly…) increases perceived loudness by a constant amount.
It is confusing. A 10 dB increase in sound pressure level does correspond to a 10x increase in power. But for a 1 kHz sound, it results in a 2x increase in perceived loudness.
Oh, hmm – that 10 dB increase (at 1 kHz) is a 10 phons increase in loudness-measured-in-phons, right? (“Loudness level in phons is defined to match sound pressure level in decibels for a 1 kHz pure tone.”)
Are phons set up so that any increase by 10 phons is a 2x increase in perceived loudness?
I’d have expected units for loudness to be set up so that a constant increase (as measured in those units) is a constant increase in perceived loudness.
Yes to your first two questions.
Thanks!
You might find that sones match your expectations better than phones.
loudness in phon = 10 log_2(loudness in sone) + 40
Makes sense. I think the main thing I find confusing is the idea of talking about some quantity without specifying units. If someone just says “loudness” without units (“At 1 kHz, loudness increases by a factor of 2 …”), I suppose most of the time I should think they mean sones / perceived loudness (equivalent).