The Hilbert transform of a function f(t) is a function fH(x) defined [1] by

The integral must be interpreted in the sense of the Cauchy principal value:

The integrand is not absolutely integrable because of the singularity at x and so the value of the integral depends on how you handle the singularity. The Cauchy principle part says to approach the singularity symmetrically.
I tried playing around with the Hilbert transform in Mathematica and ran into frustration.
I expected Mathematica would have a Hilbert transform function, but apparently it does not. It does not have a function named HilbertTransform, which would be the obvious name, and Mathematica very often gives things the obvious name.
Sine example
Next I tried showing that the Hilbert transform of sin(t) is cos(x). This is sort of a canonical example of a Hilbert transform pair, and a very useful tool in signal processing.
The direct approach doesn’t work, even though Mathematica has a way to specify that integrals should use the principle value. More on that below.
However, there is a theorem that says the Hilbert transform can be computed another way, and that worked in Mathematica.

With Mathematica I computed
Limit[
Integrate[(Sin[x + t] - Sin[x - t])/t, {t, e, Infinity}]/Pi,
e -> 0]
and it returned Cos[x].
The reason the direct approach didn’t work is that there are more subtleties than the singularity at x. The integral is also not absolutely convergent as t goes to ±∞. Rigorously defining the Hilbert transform of the sine function requires using generalized functions, a.k.a. distributions. Here’s an example of how that’s done with Fourier transforms; the development for Hilbert transforms would be analogous.
Box function example
Other common examples of Hilbert transforms also ran into difficulties when trying to derive them in Mathematica. But the box function example worked because there are no issues at infinity.
Let f(x) be the indicator function of the interval [−1, 1], the function that is 1 on the interval and 0 elsewhere. We could write this as [−1 ≤ x ≤ 1] in Iverson’s notation.
Mathematica has a function UnitBox for the indicator function of [−1/2, 1/2], so our f(x) is UnitBox[x/2].
The code
Integrate[UnitBox[t/2]/(t - x),
{t, -Infinity, Infinity},
PrincipalValue -> True] / Pi
returns
(-Log[-1 - x] + Log[1 - x]) / π
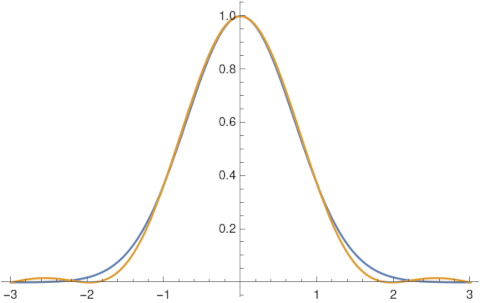
Let’s try the alternate expression we used for sine above.
Limit[
Integrate[(UnitBox[(t + x)/2] - UnitBox[(t - x)/2])/x,
{x, e, Infinity}] / Pi,
e -> 0]
This gives us a messy but similar result.
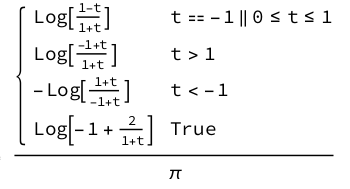
which can be written more compactly as

Related posts
[1] Some authors define the Hilbert transform to be the negative of the integral above. The inverse of the Hilbert transform works out to be the negative of the Hilbert transform, so the confusion over conventions amounts to disagreeing on which should be called the transform and which should be called the inverse.