After posting about a magic square made from knight’s tour, I wondered whether there are magic squares made from a king’s tour. (A king can move one square in any direction. A tour is a sequence of moves that lands on each square of a chess board exactly once.) I found George Jelliss’ site via the comments to that post and found out that there are indeed magic king’s tours. Here’s one published in 1917.
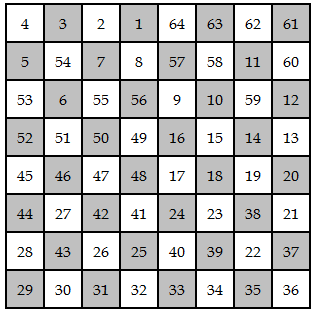
Here’s the path a king would take in the square above:

The knight’s tour magic square had rows and columns that sum to 260, though the diagonals did not. In fact, someone has proved that a knight’s tour on an 8×8 board cannot be diagonally magic. (Thanks John V.)
In the king’s tour above, however, the rows, columns, and diagonals all sum to 260. George Jelliss has posted notes that classify all such magic squares that have biaxial symmetry. See his site for much more information.

Omg, how do they construct them? Are there any smarter ways beyond brute force search? I can’t imagine how much time it would take to do direct search manually.
@Usov Clearly the solution here has some symmetry, so it could be deduced without brute force.
You mean he had to brute-force just 1/8 of a desk. Which saves quite a bit of work.
Hi John,
Thanks for the post on the magic square king’s tour. I have been fooling around with some magic square models. I made a 3D water retention graphic of your kings tour.
I solved this problem on my own fairly easily. I was constructing tours for all the chess pieces that could go on tours: kings, queens, knights and rooks. All of mine start with the number 1 in the starting position of the respective chess piece. Anyway, the pattern I found was simple.
36 35 34 33 32 31 30 29
37 38 39 40 25 26 27 28
21 22 23 24 41 42 43 44
20 19 18 17 48 47 46 45
13 14 15 16 49 50 51 52
12 11 10 9 56 55 54 53
60 59 58 57 8 7 6 5
61 62 63 64 1 2 3 4
Sorry, the spacing between the numbers looked better in the comment box.
David Mayer’s version of the king’s magic tour is the best I’ve seen. It simplifies the version published around 100 years ago ( which can be found in Pickover’s book of magic squares ), and has the additional qualities of producing a magic square with bent ( Franklin )
diagonals in addition to the normal
and the pleasing feature that any vertical zigzag also sums to M
( eg. 36 – 38 – 21 etc , or 34 – 38 – 23 etc ). On top of that, there is a pleasing left/right symmetry if we square the numbers in each cell
( bimagic ), for both direct and zigzag columns.
It should be noted however, that David’s square does not have the main diagonals summing to 260, and therefore ( like Euler’s famous knight’tour square) is only semi-magic. The original in Peckover’s book is fully magic, but lacks the vertical zigzags.