John von Neumann famously said
With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.
By this he meant that one should not be impressed when a complex model fits a data set well. With enough parameters, you can fit any data set.
It turns out you can literally fit an elephant with four parameters if you allow the parameters to be complex numbers.
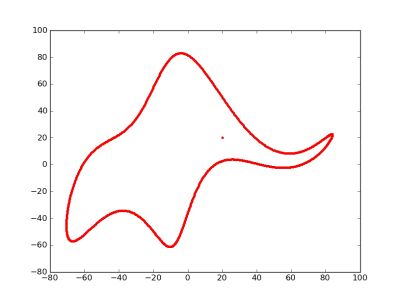
I mentioned von Neumann’s quote on StatFact last week and Piotr Zolnierczuk replied with reference to a paper explaining how to fit an elephant:
“Drawing an elephant with four complex parameters” by Jurgen Mayer, Khaled Khairy, and Jonathon Howard, Am. J. Phys. 78, 648 (2010), DOI:10.1119/1.3254017.
Piotr also sent me the following Python code he’d written to implement the method in the paper. This code produced the image above.
"""
Author: Piotr A. Zolnierczuk (zolnierczukp at ornl dot gov)
Based on a paper by:
Drawing an elephant with four complex parameters
Jurgen Mayer, Khaled Khairy, and Jonathon Howard,
Am. J. Phys. 78, 648 (2010), DOI:10.1119/1.3254017
"""
import numpy as np
import pylab
# elephant parameters
p1, p2, p3, p4 = (50 - 30j, 18 + 8j, 12 - 10j, -14 - 60j )
p5 = 40 + 20j # eyepiece
def fourier(t, C):
f = np.zeros(t.shape)
A, B = C.real, C.imag
for k in range(len(C)):
f = f + A[k]*np.cos(k*t) + B[k]*np.sin(k*t)
return f
def elephant(t, p1, p2, p3, p4, p5):
npar = 6
Cx = np.zeros((npar,), dtype='complex')
Cy = np.zeros((npar,), dtype='complex')
Cx[1] = p1.real*1j
Cx[2] = p2.real*1j
Cx[3] = p3.real
Cx[5] = p4.real
Cy[1] = p4.imag + p1.imag*1j
Cy[2] = p2.imag*1j
Cy[3] = p3.imag*1j
x = np.append(fourier(t,Cx), [-p5.imag])
y = np.append(fourier(t,Cy), [p5.imag])
return x,y
x, y = elephant(np.linspace(0,2*np.pi,1000), p1, p2, p3, p4, p5)
pylab.plot(y,-x,'.')
pylab.show()

There’s even a Mathematica widget to do this: http://demonstrations.wolfram.com/FittingAnElephant/
I have done this using R。
http://yishuo.org/?p=768
At first I thought you had come up with this yourself and I was mega-impressed, with either your creativity or abundance of free time – I’m not sure which – but I still think it is pretty cool.
But the eye is @ 20+20i!
“And I shall call him Numpy!”
Here’s a trunk wiggling version of the von Neumann elephant (animated gif): https://debris.glaciology.net/2015/09/25/sea-level-the-moon-and-frankenstein/
A link to the D.Bailey’s wiggly additions to the python code is also on that page.
jvn wouldn’t be that impressed, 4 complex parameters equal 8 real parameters..
just kidding, nice article :)
Great, I am trying out the source code now. hrm… seems I need pylab. oh… i suppose i will google pylab it for awhile. Thank You for the article.
You could make this four real parameters if have some function that first decomposes at the natural and floating parts separately.