This is a drawing of Stewart’s cube. At each corner, the sum of the weights of the incoming edges is 83. Each edge has a prime weight, and all the weights are distinct.
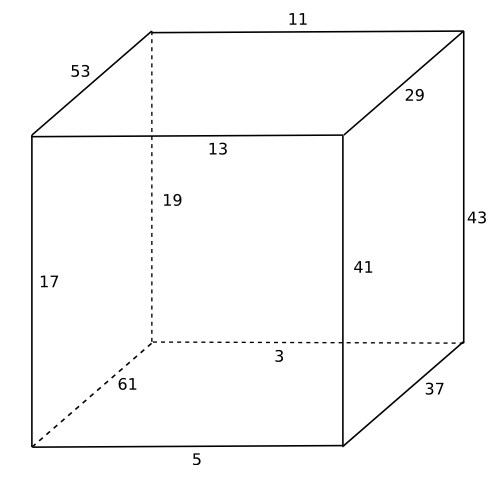
Update: See Austin Buchanan’s post. He found a similar cube with smaller primes.
Comments are closed.
Interesting…
I’m guessing Stewart had a lot of time on his hands if he figured that one out :)
I wonder if there are OTHER cubes (or cube graphs) with similar properties (distinct prime edge weights, identical sums at vertices)?
Mike: There are a lot of so-called magic graphs where the sum of the weights at each vertex is the same. However, the definition also requires the edge weights to be 1, 2, 3, …, n. So Stewart’s cube isn’t a magic graph.
John, that’s interesting, but not quite what I was pondering – I’m wondering if there are other Stewart-class (TM pending) cubes with different distinct prime edge weights and (likely) a different identical sum at the vertices.
I guess another way to state it is that you need to find a number x such that there are 8 distinct sets of primes (p1i, p2i, p3i) such that p1i+p2i+p3i == x, and the 8 (p1i, p2i, p3i) sets only have 12 distinct primes in them?
… and each p_ij appears only in two sets.
What about a hypercube version?
Left as an exercise for the reader. :) If you come up with something, let me know.
John,
Thanks for item on Stewart’s Cube, I found it most interesting. I have written a small program in C to do a search for other examples. The first cube seems to be for a target of 77. Once above target of about 100, the cubes come thick and fast. Has anyone else tried this?
MikeT: See this post from Austin Buchanan. I’m about to edit this post to point to his.
John, Do you know who, when, this Stewart is, was?