The Dirac comb or Sha function

The sha function, also known as the Dirac comb, is denoted with the Cyrillic letter sha (Ш, U+0428). This letter was chosen because it looks like how people visualize the function, a long series of vertical spikes. The function is called the Dirac comb for the same reason. This function is very important in Fourier analysis because it relates Fourier series and Fourier transforms. It relates sampling and periodization.  It’s its own Fourier transform, and with a few qualifiers discussed later, the only such function.

The Ш function, really the Ш distribution, is defined as

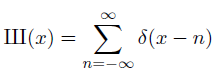
Here δ(x – n) is the Dirac delta distribution centered at n. The action of δ(x – n) on a test function is to evaluate that function at n. You can envision Ш as an infinite sequence of spikes, one at each integer. The action of Ш on a test function is to add up its values at every integer.

Sampling

The product of Ш with a function f is a new distribution whose action on a test function φ is the sum of f φ over all integers. Or you could think of the distribution as a sort of clothesline on which to hang the sampled values of f, much the way a generating function works.

Periodizing

Next let’s look at a function f that lives on [0, 1], i.e. is zero everywhere outside the unit interval. The convolution of f with δ(x – n) is f(x – n), i.e. a copy of f shifted over to live on the interval [n, n+1]. So by taking the convolution with Ш, we create copies of f all over the real line. We’ve made f into a periodic function. So instead of saying “the function f extended to create a periodic function” you can simply say f*Ш.

Fourier transform

Now let’s think about the Fourier transform of Ш. The Fourier transform of δ(x) is 1, i.e. the function equal to 1 everywhere [1].  (The more concentrated a function is, the more spread out its Fourier transform. So if you have an infinitely concentrated function δ, its Fourier transform is perfectly flat, 1. You can calculate the transform rigorously, this is the intuition.) If you shift a function by n, you rotate its Fourier transform by exp(-2πinω). So we can compute the transform of Ш:

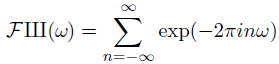
This equation only makes sense in terms of distributions. The right hand side does not converge in the classical sense; the individual terms don’t even go to zero, since each term has magnitude 1. So what kind of distribution is this thing on the right side? It is in fact the Ш function again, though this is not obvious.

To see that the exponential sum is actually the Ш function, i.e. that Ш is its own Fourier transform, we need to back up a little bit and define Fourier transform of a distribution. As usual with distributions, we take a classical theorem and turn it into a definition in a broader context.

For absolutely integrable functions, we have

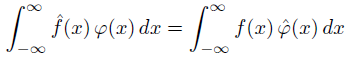
where the hat on top of a function indicates its Fourier transform. Inspired by the theorem above, we define the Fourier transform of a distribution f to be the functional whose action on a test function φ is given below.

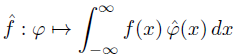
As we noted in a previous post, the integral above can be taken literally if f is a distribution associated with an ordinary function, but in general it means the application of the linear functional to the test function.

As a distribution, exp(-2πinω) acts on a test function φ by integrating against it. From the definition of a (classical) Fourier transform, this gives the Fourier transform of φ evaluated at n. So the Fourier transform of Ш acts on φ by summing the values of φ’s Fourier transform over all integers. By the Poisson summation formula, this is the same as summing the values of φ itself over all integers. Which is the same as applying Ш. So the Fourier transform of Ш has the same effect on test functions as Ш. In other words, Ш is its own Fourier transform.

Uniqueness

We haven’t been explicit about where our test functions come from. We require that xⁿ φ(x) goes to zero as x goes to ±∞ for any positive integer n. These are called functions of rapid decay. And the distributions we define as linear functionals on such test functions are called tempered distributions.

The Ш distribution is essentially unique. Any tempered distribution with period 1 that equals its own Fourier transform must be a multiple of Ш.

***

[1] All Fourier transform calculations here use the convention I call (-1, τ, 1) in these notes on various definitions. This may be the most common definition, though there are several minor variations in common use.