Hypergeometric distribution and hypergeometric functions

What’s the connection between the hypergeometric distributions, hypergeometric functions, and hypergeometric series?

The hypergeometric distribution is a probability distribution with parameters N, M, and n. Suppose you have an urn containing N balls, M red and the rest, N – M blue and you select n balls at a time. The hypergeometric distribution gives the probability of selecting k red balls.

The probability generating function for a discrete distribution is the series formed by summing over the probability of an outcome k and x^k. So the probability generating function for a hypergeometric distribution is given by

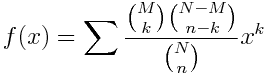
$f(x) = \sum \frac{{M\choose k}{N-M \choose n-k}}{{N \choose n}} x^k$

The summation is over all integers, but the terms are only non-zero for k between 0 and M inclusive. (This may be more general than the definition of binomial coefficients you’ve seen before. If so, see these notes on the general definition of binomial coefficients.)

It turns out that f is a hypergeometric function of x because it is can be written as a hypergeometric series. (Strictly speaking, f is a constant multiple of a hypergeometric function. More on that in a moment.)

A hypergeometric function is defined by a pattern in its power series coefficients. The hypergeometric function F(a, b; c; x) has the power series

$F(a, b; c) = \frac{(a)_k (b)_k}{(c)_k} \frac{x^k}{k!}$

where (n)_k is the kth rising power of n. It’s a sort of opposite of factorial. Start with n and multiply consecutive increasing integers for k terms. (n)₀ is an empty product, so it is 1. (n)₁ = n, (n)₂ = n(n+1), etc.

If the ratio of the k+1st term to the kth term in a power series is a polynomial in k, then the series is a (multiple of) a hypergeometric series, and you can read the parameters of the hypergeometric series off the polynomial. This ratio for our probability generating function works out to be

$\frac{P(X=k+1)}{P(X=k)} = \frac{(k-M)(k-n)}{(k+N-M-n+1)(k+1)}$

and so the corresponding hypergeometric function is F(-M, –n; N – M – n + 1; x). The constant term of a hypergeometric function is always 1, so evaluating our probability generating function at 0 tells us what the constant is multiplying F(-M, –n; N – M – n + 1; x). Now

$f(0) = P(X = 0) = \frac{{N-M \choose n}}{{N \choose n}}$

and so

$f(x) = \frac{{N-M \choose n}}{{N \choose n}} F(-M, -n; N - M - n + 1; x)$

The hypergeometric series above gives the original hypergeometric function as defined by Gauss, and may be the most common form in application. But the definition has been extended to have any number of rising powers in the numerator and denominator of the coefficients. The classical hypergeometric function of Gauss is denoted ₂F₁ because it has two falling powers on top and one on bottom. In general, the hypergeometric function _pF_q has p rising powers in the numerator and q rising powers in the denominator.

The CDF of a hypergeometric distribution turns out to be a more general hypergeometric function:

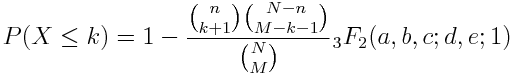
$P(X \leq k) = 1 - \frac{{n\choose k+1}{N-n\choose M-k-1}}{{N\choose M}} \phantom{ }_3F_2(1, k+1-M, k+1-n; k+2, N+k+2-M-n; 1)$

where a = 1, b = k+1-M, c = k+1-n, d = k+2, and e = N+k+2-M–n.

Thanks to Jan Galkowski for suggesting this topic via a comment on an earlier post, Hypergeometric bootstrapping.

Connection between hypergeometric distribution and series

One thought on “Connection between hypergeometric distribution and series”