What do tuning a guitar and tuning a radio have in common? Both are examples of beats or amplitude modulation.
Examples
In an earlier post I wrote about how beats come up in vibrating systems, such as a mass and spring combination or an electric circuit. Here I look at examples from music and radio.
Music
When two musical instruments play nearly the same note, they produce beats. The number of beats per second is the difference in the two frequencies. So if two flutes are playing an A, one playing at 440 Hz and one at 442 Hz, you’ll hear a pitch at 441 Hz that beats two times a second. Here’s a wave file of two pure sine waves at 440 Hz and 442 Hz.
As the players come closer to being in tune, the beats slow down. Sometimes you don’t have two instruments but two strings on the same instrument. Guitarists listen for beats to tell when two strings are playing the same note with the same pitch.
AM radio
The same principle applies to AM radio. A message is transmitted by multiplying a carrier signal by the content you want to broadcast. The beats are the content. As we’ll see below, in some ways the musical example and the AM radio example are opposites. With tuning, we start with two sources and create beats. With AM radio, we start by creating beats, then see that we’ve created two sources, the sidebands of the signal.
Mathematical explanation
Both examples above relate to the following trig identity:
cos(a − b) + cos(a + b) = 2 cos a cos b
And because we’re looking at time-varying signals, slip in a factor of 2πt:
cos(2π(a − b)t) + cos(2π(a + b)t) = 2 cos 2πat cos 2πbt
Music
In the case of two pure tones, slightly out of tune, let a = 441 and b = 1. Playing an A 440 and an A 442 at the same time results in an A 441, twice as loud, with the amplitude going up and down like cos 2πt, i.e. oscillating two times a second. (Why two times and not just once? One beat for the maximum and one for the minimum of cos 2πt.)
It may be hard to hear beats because of complications we’ve glossed over. Musical instruments are never perfectly in phase, but more importantly they’re not pure tones. An oboe, for example, has strong components above the fundamental frequency. I used a flute in this example because although its tone is not simply a sine wave, it’s closer to a sine wave than other instruments, especially when playing higher notes. Also, guitarists often compare the harmonics of two strings. These are purer tones and so it’s easier to hear beats between them.
Radio
For the case of AM radio, read the equation above from right to left. Let a be the frequency of the carrier wave. For example if you’re broadcasting on AM station 700, this means 700 kHz, so a = 700,000. If this station were broadcasting a pure tone at 440 Hz, b would be 440. This would produce sidebands at 700,440 Hz and 699,560 Hz.
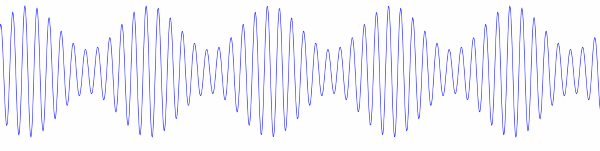
In practice, however, the carrier is not multiplied by a signal like cos 2πbt but by 1 + m cos 2πbt where |m| < 1 to avoid over-modulation. Without this extra factor of 1 the signal would be 100% modulated; the envelope of the signal would pinch all the way down to zero. By including the factor of 1 and using a modulation index m less than 1, the signal looks more like the image above, with the envelope not pinching all the way down. (Over-modulation occurs when m > 1. Instead of the envelope pinching to zero, the upper and lower parts of the envelop cross.)

Very interesting. I have not thought about these things in many years. But now it does remind me of my late dad’s short wave radio receiver. It had a big knob to adjust the BFO (beat frequency oscillator) and hear the morse code signals. Since the pulses were just on-off transmitting there was no audio signal; but the signal could be made audible by the BFO. Its generation of a constant sine wave frequency offset from the radio’s intermediate after mixing the two resulted in an audio signal that was the difference between the two frequencies. What fun it was to explore and learn about those things growing up.
I would suppose that radio, if it were still around today, would be 75 or more years old.
You seem to be describing heterodyning. https://en.wikipedia.org/wiki/Heterodyne You get the sum and difference of the 2 input signals, so 440 + 442 would yield 2Hz and 882Hz. The beat would be the difference. I’ve never heard of it being used to modulate an AM transmitter, but it is used in detecting both AM and FM by shifting the RF down to an IF (intermediate frequency) so that it can be bandpass filtered more narrowly; 455kHz for AM, 10.7 MHz for FM.
Hi John, I also found this interesting, having just taken a ham licence for very similar reasons. Actually found the exam frustrating – I would have found it so much easier to be told about impedance as a complex number with resistance and +j/-j inductive / capacitative reactance. Still, given I don’t want to become an RF engineer, I can’t grumble too much and I really only got in touch to say how much I appreciated this blog.
Hi R Van Valkenburgh, the BFO (beat frequency oscillator) was also used to make received SSB ‘single sideband’ transmissions intelligible.