This morning I was reading Terry Tao’s overview of the work of Yves Meyer and ran across this line:
The powers φ, φ2, φ3, … of the golden ratio lie unexpectedly close to integers: for instance, φ11 = 199.005… is unusually close to 199.
I’d never heard that before, so I wrote a little code to see just how close golden powers are to integers.
Here’s a plot of the difference between φn and the nearest integer:
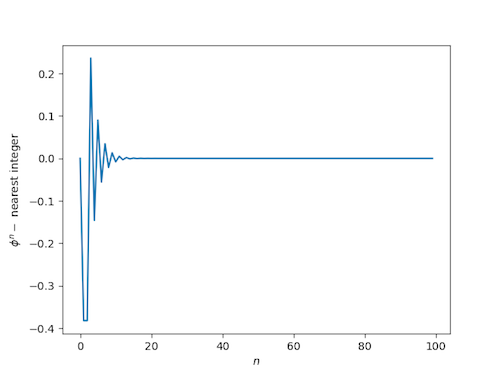
(Note that if you want to try this yourself, you need extended precision. Otherwise you’ll get strange numerical artifacts once φn is too large to represent exactly.)
By contrast, if we make the analogous plot replacing φ with π we see that the distance to the nearest integer looks like a uniform random variable:
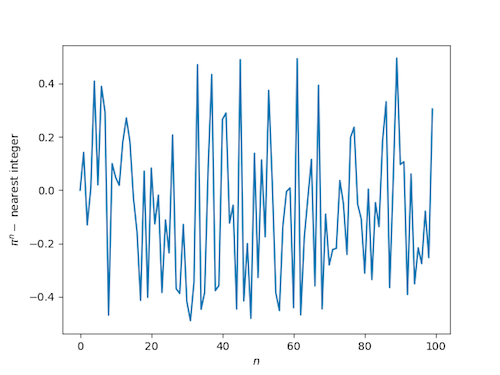
The distance from powers of φ to the nearest integer decreases so fast that cannot see it in the graph for moderate sized n, which suggests we plot the difference on the log scale. (In fact we plot the log of the absolute value of the difference since the difference could be negative and the log undefined.) Here’s what we get:
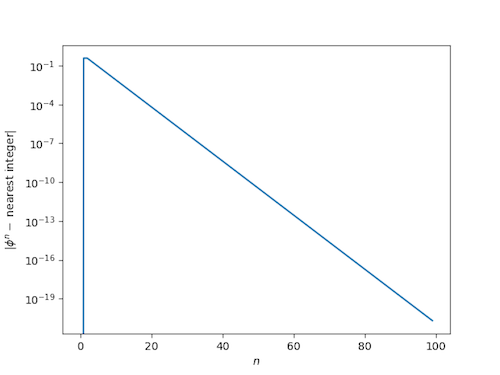
After an initial rise, the curve is apparently a straight line on a log scale, i.e. the absolute distance to the nearest integer decreases almost exactly exponentially.

This happens because phi^n + (-phi)^(-n) is always an integer (you can prove this by induction in n). Hence the log of the absolute value of the difference being linear (it’s -n*log(phi).)
In this sense, phi is not so special; you can also try, for instance, 2+sqrt(3), or the largest root of a quadratic x^2 + ax + b = 0, a, b integers, such that the smallest root has absolute value smaller than 1.
This follows trivially from Binet’s formula for Fibonacci numbers.
Carlos and Theemathas:
Let x_n = phi^n + (-phi)^(-n). I see why x_n/sqrt(5) is near an integer — in fact it’s exactly an integer, the nth Fibonacci number — but I don’t see why x_n itself should be near an integer. Said another way, why should sqrt(5) times a Fibonacci number be nearly an integer?
Start with 1/√5 instead of 1 when repeatedly multiplying the powers of φ and near integers are also generated… although they’ll be a lot more familiar than the ones generated here (which are also fairly well known as it happens).
I have what I would consider an [moderately] unsurprising inductive proof of this convergence towards integers. Recall that the nth fibonacci number $f_n = \frac{\phi^n – (–\phi)^{–n}}/{\sqrt{5}}$. Since the second term decays exponentially, call that term $\epsilon_n$. Then we can say $\phi^n = \sqrt{5}(F_n – \epsilon_n)$. Now, the induction hypotheses are that for two consecutive n we have $\phi^n = z_n – (-1)^{n} \delta_n$ where $z_n$ is an integer and $\delta_n$ is positive and decreasing with n, and obeys a condition explained below.
Write $\phi^{n+1} = (F_{n+1} – \epsilon_{n+1})\sqrt{5}$. Use $F_{n+1}=F_n+F_{n–1}$ and substitute back to get $\phi^{n+1} = ( \phi^n/\sqrt{5} + \phi^{n-1}/\sqrt{5} + \epsilon_n + \epsilon_{n–1} – \epsilon_{n+1})\sqrt{5}$. The sum of the epsilons is exactly zero! So the square-roots of 5 cancel, and now invoke the induction hypothesis. $\phi^{n+1} = z_n + z_{n_1} – (-1)^{n} \delta_n – (-1)^{n–1} \delta_{n–1}$. So, we see $z_{n+1}$ is just $z_n + z_{n+1}$, and careful tracking of signs shows that $\delta_{n+1} = (\delta_{n-1} – \delta_n)$.
If $\delta_n > \delta_{n-1}/2$, then $\delta_{n+1} \delta_n > \delta_{n-1}/2$.
So now we just need to hunt for a pair of $n$s that form the base case. $\phi^2$ is $\delta_2=0.3819…$ less than 3 while $\phi^3$ is $\delta_3=0.236…$ more than 4, and $3/4 \delta_{3} > \delta_4 > \delta_{3}/2$. This completes the proof that the deltas decrease with n and so $\phi^n$ is very nearly an integer.
Now, showing that it exponentially decays can be seen by examining the difference equation for $\delta$. Rewrite it as $\delta_n = -(\delta_{n+1} – \delta_{n-1})$ This is the finite difference approximation of the differential equation $\delta(x) = -2 \partial_x \delta(x)$ which is solved by $\delta(x) = c \exp(-x/2)$ with some c, and 1/2 is VERY nearly the slope in your plot!
Sorry, I had sloppy copy-and-pasting. The third paragraph (about the inequalities between deltas) should read:
If $\delta_n > \delta_{n-1}/2$, then $\delta_{n+1} \delta_n > \delta_{n-1}/2$.
Nope, it’s a problem with the comments. After what’s above, it should read:
But we also now need to induce on this hypothesis, and we wind up with the requirement that $3 \delta_{n-1}/4 > \delta_n > \delta_{n-1}/2$.
It is easier in the following way:
If x(0)=a+b and x(1)=a*phi+b/(-phi) are integer then x(n)=a*phi^n+b/(-phi)^n will always be integer. This is because phi and -1/phi are the two solutions of x^2=x+1, and thus x(n+1)=x(n)+x(n-1) for all n.
Comment was sent before it was finished, and I cannot edit it. So here it goes on:
This does not help, however, to solve the problem. We would need a=1, and thus an integer b, and then phi-b/phi can not be integer, for that means b=phi^2-c*phi=1+(1-c)*phi.
@Rene, what’s wrong with a = b = 1? x(0) = 2, x(1) = phi – 1/phi = 1. Then phi^n + 1/(–phi)^n is always integer, and the second term decays.
And, @Renee, if b=1 then \delta_n (in my language) is 1/phi^n (I had pulled the minus sign out explicitly). That explains why the slope in John’s plot isn’t exactly -1/2, but is a little bit more— log(1/phi) = -0.481212… Your way is indeed beautiful.
The numbers x_n = phi^n + (-phi)^(-n) mentioned above are called Lucas numbers, see https://en.wikipedia.org/wiki/Lucas_number
Even more generally, this happens for any real algebraic number greater than 1 all of whose complex conjugates are inside the complex unit circle. For example, the root of z^3-z-1 that is close to 1.32 has its powers getting close to an integer. These are called PV-numbers. https://en.wikipedia.org/wiki/Pisot%E2%80%93Vijayaraghavan_number
Another simple way to understand this is that, if F(n) is the nth fibonacci number with F(0) = 0, F(1) = 1, then using the fact that \phi^2 = \phi + 1, it’s an easy induction to show that \phi^n = F(n)\phi + F(n-1).
Since the ratio of consecutive fibonacci numbers approaches \phi, we have for large n that F(n)\phi ≈ F(n+1), so that \phi^n ≈ F(n+1) + F(n-1)
Very cool, I didn’t know this fact. I once computed Phi to 2,000+ digits using a Matlab program of my own invention. I used FFTs for high precision floating
point multiplication simulation and Newton’s iteration for division (inverses). I used the ratio of Fibonacci numbers method and then the direct formula for Phi as a check. The latter method was faster of course, but only took a few seconds on a 2 GHz PC!
Gary Sitton
DSP Consultant
Houston, TX
Do you have the code you used to make these graphs on git by chance?
For every odd integer n >= 479, the fractional part of Phi^n is less than 1/Googol (10^100).
Try Table[Simplify[(1/2^n) (Expand[(1 + Sqrt[5])^n] +
Expand[(1 – Sqrt[5])^n])], {n, 0, 10}] in Mathematica.
THANKS MUCHLY Mr Cook / John. “Golden powers are nearly integers” is a beautiful presentation. I especially like/enjoy the plot + log-plot as it’s like an empirical (engineering signals analysis) waveform. So the pattern of your plot is very cool. .. *** John would I be able to have a copy of the (?python) code which you used in your making your presentation *** .. I am a retiring biomedical engineer interested in STEM teaching for underprivileged kids + I will do ethical thing, ie NOT circulate your code / teaching purposes ONLY .. If you say no I respectfully understand.
There are lots of numbers that behave like this. They are called Pisot numbers and you can read about them here: http://mathworld.wolfram.com/PisotNumber.html or on wikipedia.
The following code in python might do it
from decimal import * getcontext().prec = 100 import matplotlib.pyplot as plt data = [] phi = (1 + Decimal(5).sqrt())/2 for n in range(0,100): phi_n = phi**n data.append(phi_n - phi_n.to_integral_value()) plt.plot(data) plt.show() plt.plot([abs(datum).log10() for datum in data]) plt.show()