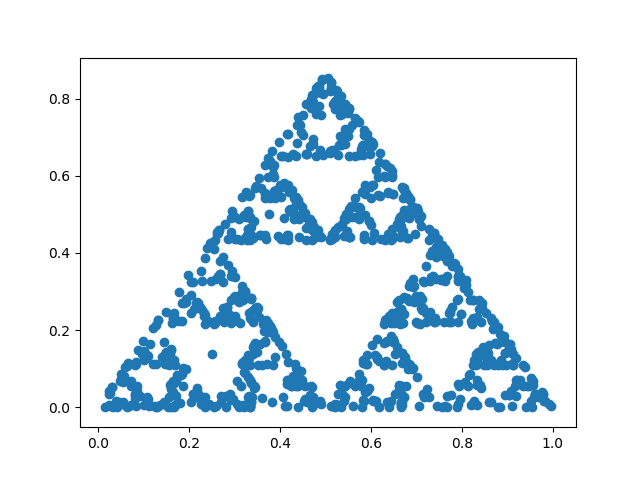
The chaos game is played as follows. Pick a starting point at random. Then at each subsequent step, pick a triangle vertex at random and move half way from the current position to that vertex.
The result looks like a fractal called the Sierpinski triangle or Sierpinski gasket.
Here’s an example:
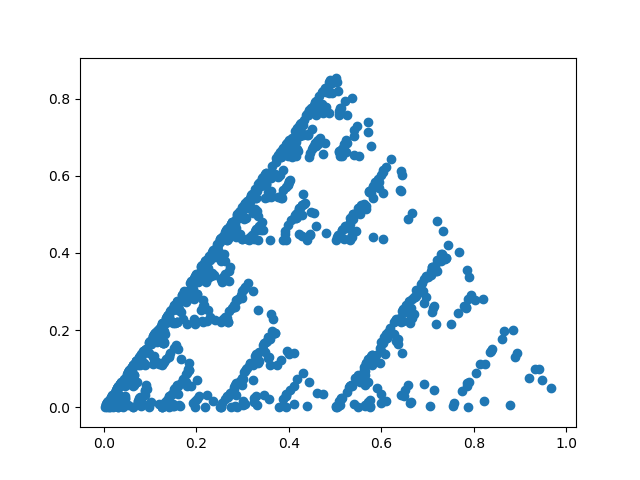
If the random number generation is biased, the resulting triangle will show it. In the image below, the lower left corner was chosen with probability 1/2, the top with probability 1/3, and the right corner with probability 1/6.
Update: Here’s an animated version that lets you watch the process in action.
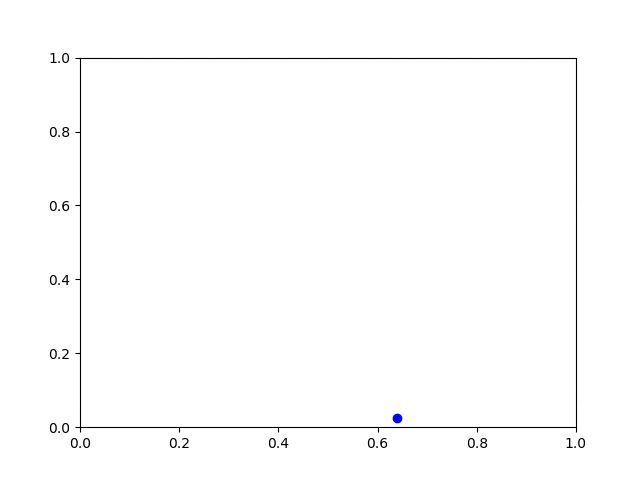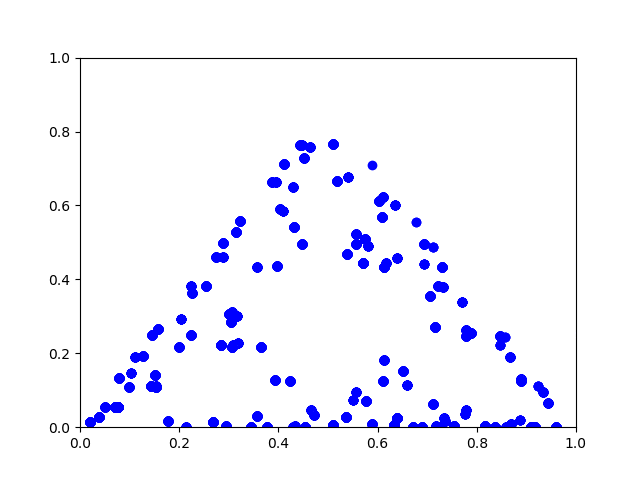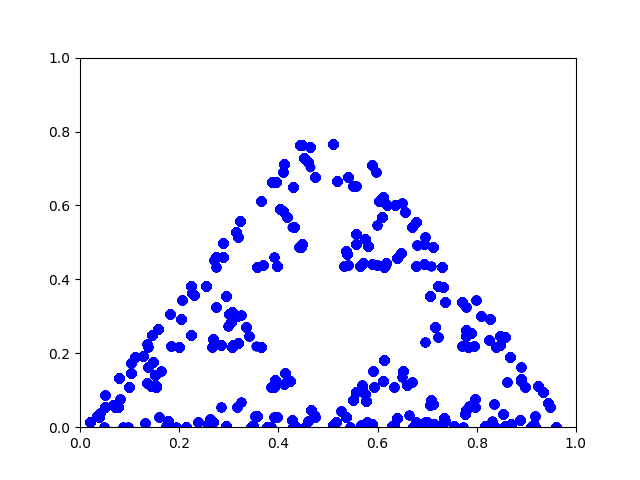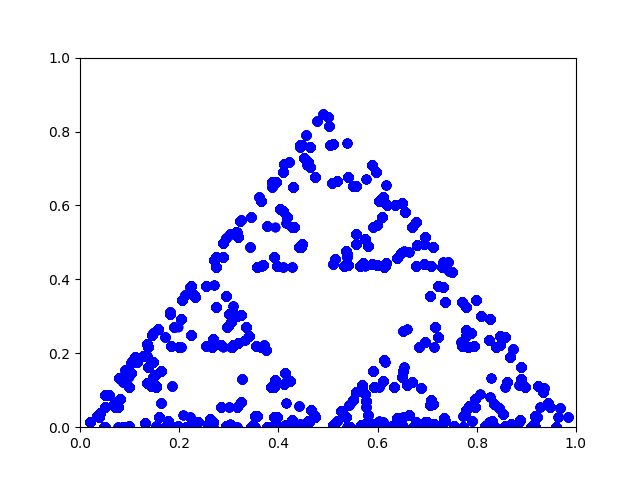
Here’s Python code to play the chaos game yourself.
from scipy import sqrt, zeros
import matplotlib.pyplot as plt
from random import random, randint
def midpoint(p, q):
return (0.5*(p[0] + q[0]), 0.5*(p[1] + q[1]))
# Three corners of an equilateral triangle
corner = [(0, 0), (0.5, sqrt(3)/2), (1, 0)]
N = 1000
x = zeros(N)
y = zeros(N)
x[0] = random()
y[0] = random()
for i in range(1, N):
k = randint(0, 2) # random triangle vertex
x[i], y[i] = midpoint( corner[k], (x[i-1], y[i-1]) )
plt.scatter(x, y)
plt.show()
Update 2: Peter Norvig posted some Python code with variations on the game presented here, generalizing a triangle to other shapes. If you try the analogous procedure with a square, you simply get a square filled with random dots.
However, you can get what you might expect, the square analog of the Sierpinski triangle, the product of a Cantor set with itself, if you make a couple modifications. First, pick a side at random, not a corner. Second, move 1/3 of the way toward the chosen side, not 1/2 way.
Here’s what I got with these changes:
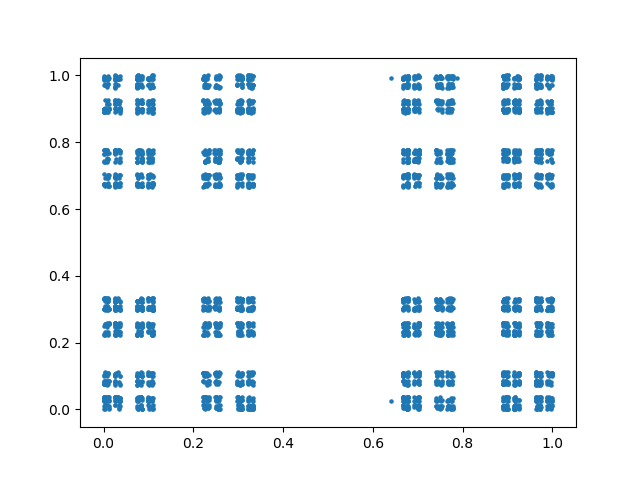
Source: Chaos and Fractals

Here is my golfed-down JS version: https://jsfiddle.net/ondras/XVNFe/
What fun! I played another few moves in the game: https://github.com/norvig/pytudes/blob/master/Sierpinski.ipynb
As a complete ignoramus, I get a kick out of seeing really smart guys just having fun with math.
Thanks!
I should have said this explicitly, but I got the game from the book referenced at the bottom of the post. I just illustrated it with the code and images.
You can also play the chaos game with the Julia set formula, z -> z²+ c.
Inverting this formula gives you √(z – c). There are two square roots in the complex plane. Pick one at random.
Is there a way to quantify how fast the points converge on lying exactly on the Sierpinski triangle?
Interesting! Continued on this theme using fractional steps instead of midpoints; and then letting the ratio go negative.
https://github.com/cdragun/python-progs/blob/master/Sierpinski.ipynb
What if you did a star shape?
A lot of variations and theory in Barnsley’s “Fractals everywhere”
You can do a similar Chaos game for Julia sets by choosing randomly between the two square roots of a number! The inverse of the Julia iterator converges to the boundary of the julia set.
Use the mapping z -> +/- sqrt(z-c) with a random choice of the two branches of arctan on [0,2pi) and you get the wonderful result!
cx = a , cy=b, zx = 0, zy = 0; # c = a + ib, z = 0
while (1) {
tmpx = zx – cx, tmpy = zx – cy;
# Convert z into polar coordinates to make it easier to square root
r = sqrt(tmpx^2 + tmpy^2);
theta = arctan(tmpx/tmpy);
# Take square roots
new_r = sqrt(r), new_theta = theta/2;
# Choose theta/2 or theta/2 + pi as new angle randomly
if (random()%2=1) new_theta = new_theta + pi/2;
#or whatever – it’s pseudocode :-)
zx = r cos(theta); zy = r sin(theta);
plot (zx, zy);
}
Change the scipy import due to deprecation:
from numpy import zeros
from numpy import sqrt