A uniformly distributed sequence

If you take the fractional parts of the set of numbers {n cos nx :  integer n > 0} the result is uniformly distributed for almost all x. That is, in the limit, the number of times the sequence visits a subinterval of [0, 1] is proportional to the length of the interval. (Clearly it’s not true for all x: take x = 0, for instance. Or any rational number times π.)

The proof requires some delicate work with Fourier analysis that I’ll not repeat here. If you’re interested in the proof, see Theorem 4.4 of Uniform Distribution of Sequences.

This is a surprising result: why should such a strange sequence be uniformly distributed? Let’s look at a histogram to see whether the theorem is plausible.

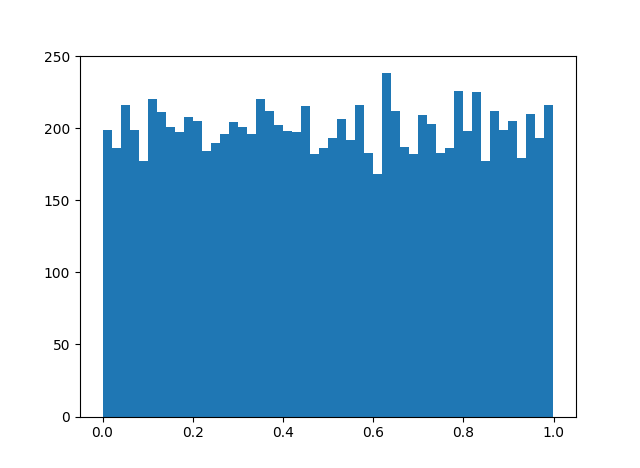
OK. Looks plausible.

But there’s a generalization that’s even more surprising. Let a_n be any increasing sequence of integers. Then the fractional parts of a_n cos a_nx are uniformly distributed for almost all x.

Any increasing sequence of integers? Like the prime numbers, for example? Apparently so. The result produces a very similar histogram.

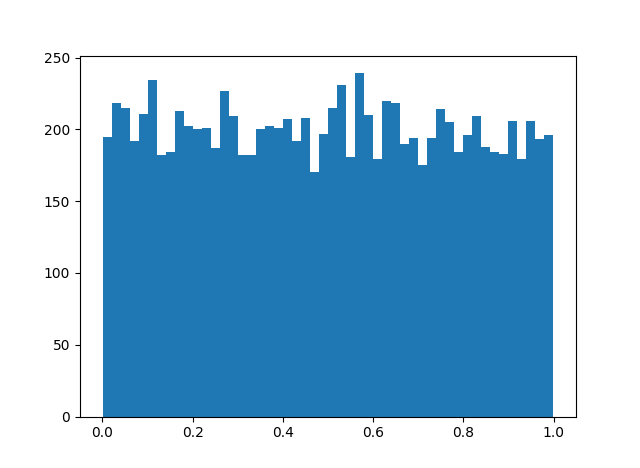
But this can’t hold for just any sequence. Surely you could pick an integer sequence to thwart the theorem. Pick an x, then let a_n be the subset of the integers for which n cos nx < 0.5. Then a_n cos a_nx isn’t uniformly distributed because it never visits the right half the unit interval!

Where’s the contradiction? The theorem doesn’t start by saying “For almost all x ….” It starts by saying “For any increasing sequence a_n ….” That is, you don’t get to pick x first. You pick the sequence first, then you get a statement that is true for almost all x. The theorem is true for every increasing sequence of integers, but the exceptional set of x‘s may be different for each integer sequence.