The exponential sum of the day draws a line between consecutive partial sums of
where m, d, and y are the current month, day, and two-digit year. The four most recent images show how different these plots can be.
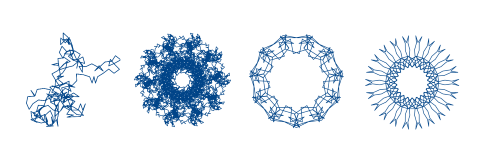
These images are from 10/30/17, 10/31/17, 11/1/17, and 11/2/17.
Consecutive dates often produce very different images for a couple reasons. First, consecutive integers are relatively prime. From a number theoretic perspective, 30 and 31 are very different, for example. (This touches on the motivation for p-adic numbers: put a different metric on integers, one based on their prime factorization.)
The other reason consecutive dates produce qualitatively different images is that you might roll over a month or year, such as going from October (10) to November (11). You’ll see a big change when we roll over from 2017 to 2018.
The partial sums are periodic [1] with period lcm(m, d, y). The image for 10/31/17 above has the most points because 10, 31, and 17 are relatively prime. It’s also true that 11, 2, and 17 are relatively prime, but these are smaller numbers.
You could think of the month, day, and year components of the sum as three different gears. The sums repeat when all three gears return to their initial positions. In the image for yesterday, 11/1/17, the middle gear is effectively not there.
[1] The terms of the sums are periodic. The partial sums are periodic if the full sum is zero. So if the partial sums are periodic, the lcm is a period.

1- Am I allowed to feel a little irritated that they ordered it m-d-y, and not d-m-y? I guess it makes for more dramatic day-to-day transitions, but had they gone d-m-y you might be able to see some common ‘theme’ over each month.
2- I haven’t yet figured out what determines whether or not the final image set has any symmetries. I’d assumed they all would, so 10/30/17 was a surprise. The obvious conjecture is “one parameter divides another”, so I guess we’ll get a lot of good (counter?)-examples come the first week of December.
I tried several permutations of m, d, and y, and chose the one that I thought made the most interesting sequence. I don’t remember anymore how the other orders differed.
It seems there is not an RSS feed for https://www.johndcook.com/expsum/
Any possibility of one?
That’s a good idea, but there’s no RSS feed.
Oh, I hadn’t realized that you were the one who created it. Apologies for ‘them-ing’ you.