Yogi Berra meets Pafnuty Chebyshev

Posted on by John

I just got an evaluation copy of The Best Writing on Mathematics 2017. My favorite chapter was Inverse Yogiisms by Lloyd N. Trefethen.

Trefethen gives several famous Yogi Berra quotes and concludes that

Yogiisms are statements that, if taken literally, are meaningless or contradictory or nonsensical or tautological—yet nevertheless convey something true.

An inverse yogiism is the opposite,

[a] statement that is literally true, yet conveys something false.

What a great way to frame a chapter! Now that I’ve heard the phrase, I’m trying to think of inverse yogiisms. Nothing particular has come to mind yet, but I feel like there must be lots of things that fit that description. Trefethen comes up with three inverse yogiisms, and my favorite is the middle one: Faber’s theorem on polynomial interpolation.

Faber’s theorem is a non-convergence result for interpolants of continuous functions. Trefethen quotes several numerical analysis textbooks that comment on Faber’s theorem in a way that implies an overly pessimistic interpretation. Faber’s theorem is true for continuous functions in general, but if the function f  being interpolated is smooth, or even just Lipschitz continuous, the theorem doesn’t hold. In particular, Chebyshev interpolation produces a sequence of polynomials converging to f.

A few years ago I wrote a blog post that shows a famous example due to Carle Runge that if you interpolate f(x) = 1/(1 + x²) over [-5, 5] with evenly spaced nodes, the sequence of interpolating polynomials diverges. In other words, adding more interpolation points makes the fit worse.

Here’s the result of fitting a 16th degree polynomial to f  at evenly spaced nodes.

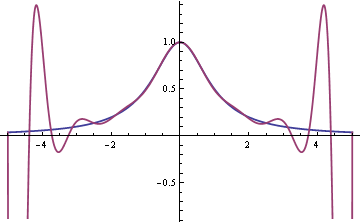
graph of f(x) and p16(x)

The error near the ends is terrible, though the fit does improve in the middle. If instead of using evenly spaced nodes you use the roots of Chebyshev polynomials, the interpolating polynomials do in fact converge, and converge quickly. If the kth derivative of f has bounded variation, then the error in interpolating f at n points is O(n–k).

2 thoughts on “Yogi Berra meets Pafnuty Chebyshev”

  1. Thanks for writing about this book. Not sure my maths is up to it, but I really like the concept of “literally true but conveys something false”. For me, some unintuitive statistical results fall into this category — I’m thinking especially of Simpson’s paradox (e.g. asking ‘which predictor is better’ in my write up https://agilescientific.com/blog/2011/3/21/confounded-paradox.html) and the Tversky–Kahneman taxicab problem (e.g. when stating the accuracy of a test as in https://agilescientific.com/blog/2011/6/29/reliable-predictions-of-unlikely-geology.html).

Comments are closed.