Shannon wavelet

The Shannon wavelet has an interesting plot:

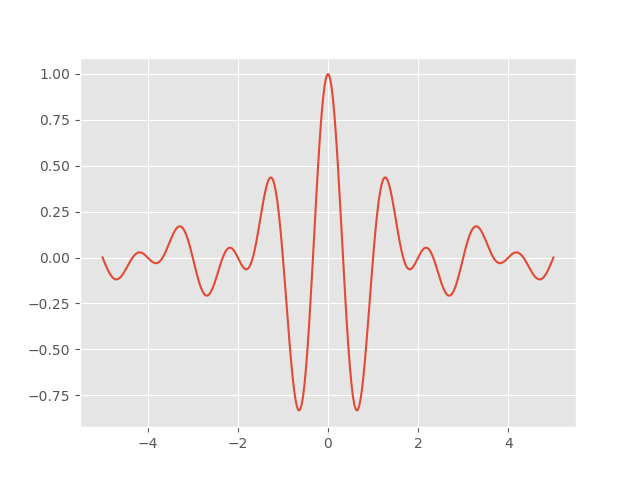
Given the complexity of the plot, the function definition is surprisingly simple:

The Fourier transform is even simpler: it’s the indicator function of [-2π, -π] ∪ [π, 2π], i.e. the function that is 1 on the intervals [-2π, -π] and [π, 2π] but zero everywhere else.

The Shannon wavelet is orthogonal to integer translates of itself. This isn’t obvious in the time domain, but it’s easy to prove in the frequency domain using Parseval’s theorem.

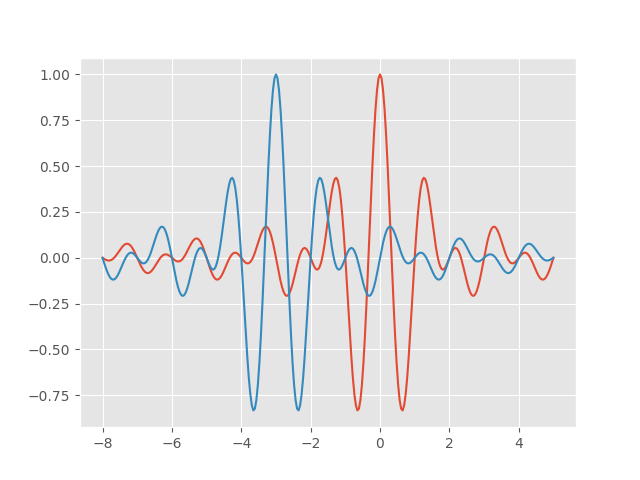
Here’s a plot of the original wavelet and the wavelet shifted to the left by 3:

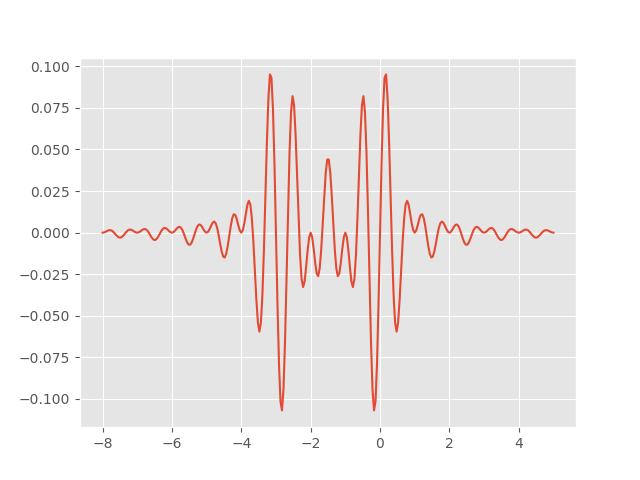
And here’s a plot of the product of the two wavelets. It’s plausible that the areas above and below the x-axis cancel out each other, and indeed they do.

Related post: Sinc and Jinc integrals