Differential privacy adds Laplace-distributed random noise to data to protect individual privacy. Although it’s simple to generate Laplacian random values, the Laplace distribution is not always one of the built-in options for random number generation libraries.
The Laplace distribution with scale β has density
The Laplace distribution is also called the double exponential because it looks like two mirror-image exponential distributions glued together.
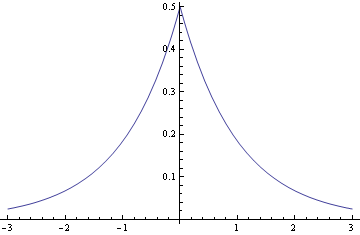
Note that the scale β is not the standard deviation. The standard deviation is √2 β.
To generate samples from a Laplace distribution with scale β, generate two independent exponential samples with mean β and return their difference.
If you don’t have an API for generating exponential random values, generate uniform random values and return the negative of the log. That will produce exponential values with mean 1. To make random values with mean β, just multiply the results by β.
If you want to generate Laplace values in Python, you could simply use the laplace function in scipy.stats. But I’ll write a generator from scratch just to show what you might do in another environment where you didn’t have exponential or Laplace generators.
from math import log
from random import random
def exp_sample(mean):
return -mean*log(random())
def laplace(scale):
e1 = exp_sample(scale)
e2 = exp_sample(scale)
return e1 - e2
Related: Stand-alone numerical code, useful when you need a few common mathematical functions but are in an environment that doesn’t provide them, or when you want to avoid adding a library to your project.

There is a bug in your code – because random.random() returns result in the [0…1) range, occasionally you’ll get FP exception due to log(0).
To fix the problem use
def exp_sample(mean):
return -mean*log(1.0 – random())