Three things about dominoes

Posted on by John

Here are three things about dominoes, two easy and one more advanced.

Counting

First, how many pieces are there in a set of dominoes? A domino corresponds to an unordered pair of numbers from 0 to n. The most popular form has n = 6, but there are variations with other values of n. You can show that the number of dominoes is

{ n+1\choose 2} + n + 1

This is because there are n+1 possible numbers (since blanks are a possibility) and each one is either a double or not. The number of ways to choose two distinct numbers is the binomial coefficient and the number of doubles is n+1.

Another way to look at this is that we are selecting two things from a set of n+1 things with replacement and so the number of possibilities is

\left({ n+1\choose 2}\right) = {n+2 \choose 2}

where the symbol on the left is Stanley’s symbol for selection with replacement.

In any case, there are 28 dominoes when n = 6, 55 when n = 9, and 91 when n = 12.

Magic squares

There are a couple ways to make a magic square of sorts from a set of dominoes. To read more about this, see this post.

Domino magic square

Tiling

How many ways can you cover an m by n chess board with dominoes? The answer turns out to be

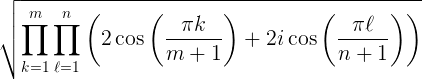
\sqrt{\prod_{k=1}^m \prod_{\ell=1}^n \left( 2\cos\left(\frac{\pi k}{m+1} \right) + 2i \cos\left(\frac{\pi \ell}{n+1} \right) \right)}

See this post for details.

2 thoughts on “Three things about dominoes”

  1. Phil

    I see it differently (for example a double 9 set) I look at the blanks (b) and of course there’s 10 consisting of bb,b1,b2…b9 then consider the 1’s 1b,11,12,13…19 now of course 1b is the same as b1 so there’s one less here that’s 9, notice every new set begins at the double of that set (the lower numbers being already counted in the previous sets)…so there’s 10 (bb-b9), the 9 (11->19), then 8 (22->29) then 7,6,5,4,3,2,1 with that last being double 9 (99)….total count is sum n from 1 to n+1 for the 9’s set that’s 55 (same as 1/2*(n+1) * (n+2)) simple no? 12 set = 1/2 * 13 * 14 = 91
    So that’s simply the triangle number from n+1…little Gauss again

  2. John Pinkerton

    Yet another way to visualize counting the dominoes is to think of choosing 2 of the following n+2 items: 0,1,2,…n,D. Where D stands for doubling the other number.
    I don’t immediately see how to generalize this conception as well as the urns and balls approach when choosing more than 2. One other small point–the version of the stars and bars visualization we learned simply had n-1 bars, allowing stars on either end without the need to visualize static bars there.

Comments are closed.