Julian Havil writes what I think of as serious recreational mathematics. His books are recreational in the sense that they tell a story rather than cover a subject. They are lighter reading than a text book, but require more advanced mathematics than books by Martin Gardner.
Havil’s latest book is Curves for the Mathematically Curious. At the end of the book, Havil presents something like a quine created by Jeff Tupper. A quine is a computer program that when executed produces its own source code. Here we have a mathematical inequality that creates an image of itself.
For 0 ≤ x < 106 and N ≤ y < N + 17, fill in a square with coordinates (x, y) if and only if
Jeff Tupper published a value of N such that the resulting image is
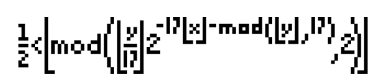
Any image of size 106 by 17 can be produced by using the right value of N. Havil uses a value of N that produces the title of his new book. Two images, actually. The title of his book is a little long for 106 pixels, so he splits it into two images. The values of N that produce Tupper’s original image and Havil’s two images have 544 digits. Havil explains how to compute N from a desired image.

Related:
https://www.youtube.com/watch?v=_s5RFgd59ao
Here is a true mathematical quine where all is included in the graph it produces, including the big number: http://jtra.cz/stuff/essays/math-self-reference/index.html
This quine is bitmap based and it looks coarse when zoomed, but there are ways to do this without bitmaps (more complex though): http://jtra.cz/stuff/essays/math-self-reference-smooth/index.html