The Brothers Markov

The Markov brother you’re more likely to have heard of was Andrey Markov. He was the Markov of Markov chains, the Gauss-Markov theorem, and Markov’s inequality.

Andrey had a lesser known younger brother Vladimir who was also a mathematician. Together the two of them proved what is known as the Markov Brothers’ inequality to distinguish it from (Andrey) Markov’s inequality.

For any polynomial p(x) of degree n, and for any non-negative integer k, the maximum of the kth derivative of p over the interval [-1, 1] is bounded by a constant times the maximum of p itself. The constant is a function of k and n but is otherwise independent of the particular polynomial.

In detail, the Markov Brothers’ inequality says

Andrey proved the theorem for k = 1 and his brother Vladimir generalized it for all positive k.

The constant in the Markov Brothers’ inequality is the smallest possible because the bound is exact for Chebyshev polynomials [1].

Let’s look at an example. We’ll take the second derivative of the fifth Chebyshev polynomial.

T₅(x) = 16x⁵ – 20x³ + 5x.

The second derivative is

T₅”(x) = 320x³ – 120x.

Here are their plots:

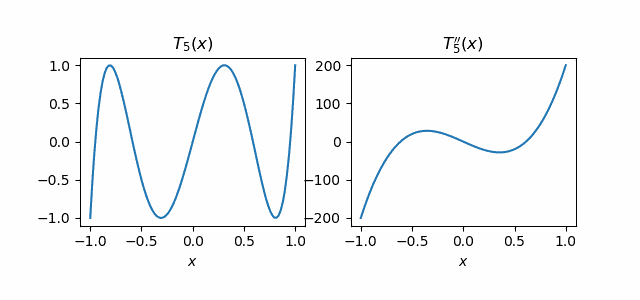
The maximum of T₅(x) is 1 and the maximum of its second derivative is 200.

The product in the Markov Brothers’ inequality with n = 5 and k = 2 works out to

(25/1)(24/3) = 200

and so the bound is exact for p(x) = T₅(x).

***

It took a while for westerners to standardize how to transliterate Russian names, so you might see Andrey written as Andrei or Markov written as Markoff.

There were even more ways to transliterate Chebyshev, including Tchebycheff, Tchebyshev, and Tschebyschow. These versions are the reason Chebyshev polynomials [1] are denoted with a capital T.

More posts mentioning Markov

• Addition carries form a Markov chain
• Markov chain Monte Carlo
• Markov’s inequality and six-sigma events
• Linear regression and the Gauss-Markov theorem

[1] There are two families of Chebyshev polynomials. When used without qualification, as in this post, “Chebyshev polynomial” typically means Chebyshev polynomial of the first kind. These are denoted T_n. Chebyshev polynomials of the second kind are denoted U_n.