I’ve written several times about the “squircle,” a sort of compromise between a square and a circle. It looks something like a square with rounded corners, but it’s not. Instead of having flat sizes (zero curvature) and circular corners (constant positive curvature), the curvature varies continuously.
A natural question is just what kind of circle approximates the corners. This post answers that question, finding the radius of curvature of the osculating circle.
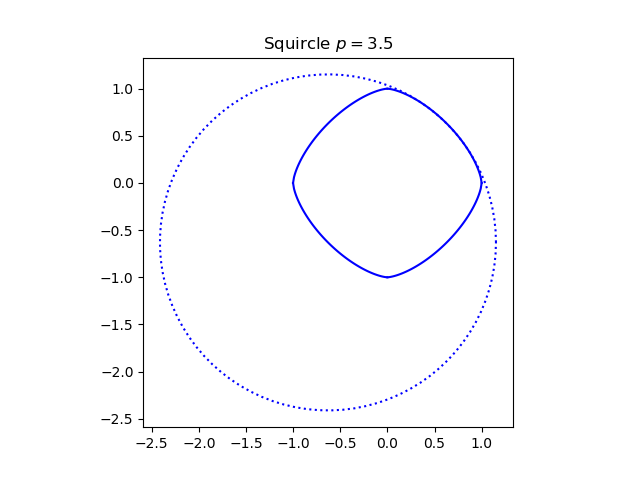
The squircle has a parameter p which determines how close the curve is to a circle or a square.
The case p = 2 corresponds to a circle, and in the limit as p goes to infinity you get a square.
We’ll work in the first quadrant so we can ignore absolute values. The curvature at each point is complicated [1] but simplifies in the corner to
and the radius of curvature is the reciprocal of this. So for moderately large p, the radius of curvature is approximately √2/(p-1).
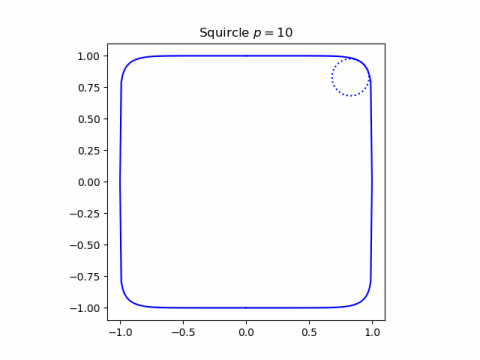
In the image at the top of the post, p = 3.5. Here’s an image with a larger value of p, p = 10.
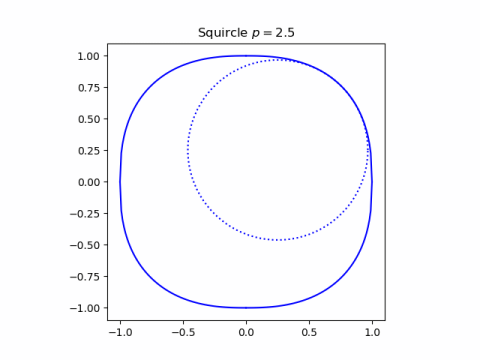
And here’s one with a smaller value, p = 2.5.
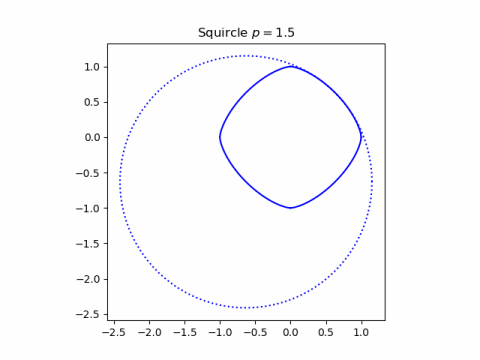
When p = 2 we get a circle. When p is between 1 and 2 we get more of a diamond than a square. Notice in the image below with p = 1.5 the osculating circle is larger than the squircle, and the “corner” is nearly the whole side.
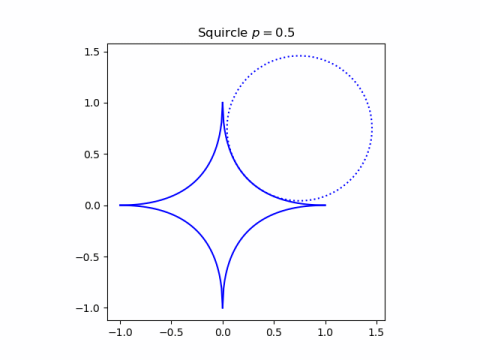
Finally, for p between 0 and 1 the sides of the diamond cave in giving a concave shape. Now the osculating circle is on the outside.
Related posts
[1] The general expression is
