Curvature is a measure of how tightly a curve bends. A circle of radius r has curvature 1/r. So a small circle has high curvature and a big circle has small curvature.
In general the curvature of a curve at a point is defined to be the curvature of the circle that best fits at that point. This circle is called the osculating circle which means the circle that “kisses” the curve at that point.
From Online Etymology Dictionary:
osculate (v.) “to kiss (one another),” 1650s, from Latin osculatus, past participle of osculari “to kiss,” from osculum “a kiss; pretty mouth, sweet mouth,” literally “little mouth,” diminutive of os “mouth”
The center of the osculating circle is called the center of curvature and the radius of the circle is called the radius of curvature.
I’ll give two examples. The first is a set of ellipses that all have the unit circle as their osculating circle on the left end. So they all have curvature 1.
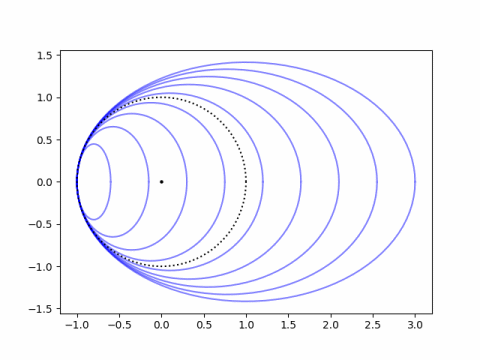
An ellipse with equation
has varying curvature at each point. At x = –a the curvature simplifies to a/b². So to make the graph above, I used a range of values for a and set each corresponding value of b to √a.
Next, instead of fixing the osculating circle I’ll fix the curve. I’ll use the equation to fit an egg that I’ve used before and plot the osculating circles at each end. The plot below uses a = 3, b = 2, and k = 0.1.
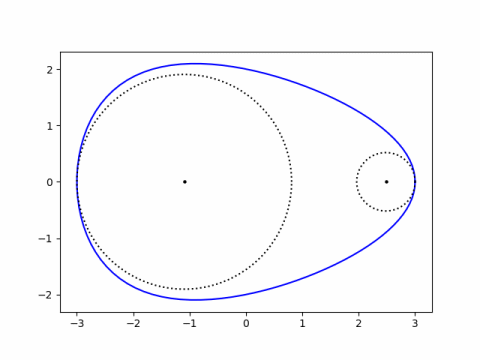
The curvature at the fat end is a(1-ka)/b² and the curvature at the pointy end is a(1+ka)/b². These are derived here.
Setting k = 0 gives the curvature of an ellipse at each end used above.

Hi John, you could enable readers to calculate and draw their own osculating circles to a curve defined by y=f(x) by mentioning
Radius = (1+y’^2)^(3/2) / |y”|
(with limits where y’->infinity).