There’s more than one way to sum an infinite series. Cesàro summation lets you compute the sum of series that don’t have a sum in the classical sense.
Suppose we have an infinite series
The nth partial sum of the series is given by
The classical sum of the series, if it exists, is defined to be the limit of its partial sums. That is,
Cesàro summation takes a different approach. Instead of taking the limit of the partial sums, it takes the limit of the averages of the partial sums. To be specific, define
and define the Cesàro summation to be the limit of the Cn as n goes to infinity. If a series has a sum in the classical sense, it also has a sum in the Cesàro sense, and the limits are the same. But some series have a Cesàro sum that do not have a classical sum. Or maybe both limits exist but the intermediate steps of Cesàro summation are better behaved, as we’ll see in an example below.
If you express the Cn in terms of the original an terms you get
In other words, the nth Cesàro partial sum is a reweighting of the classical partial sums, with the weights changing as a function of n. Note that for fixed i, the fraction multiplying ai goes to 1 as n increases.
Fejér summation and Gibbs phenomenon
Fejér summation is Cesàro summation applied to Fourier series. The (ordinary) partial sums of a Fourier series give the best approximation to a function as measured by least squares norm. But the Cesàro partial sums may be qualitatively more like the function being approximated. We demonstrate this below with a square wave.
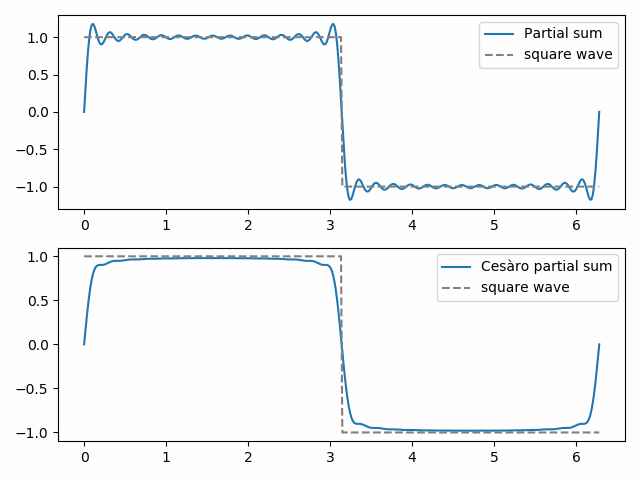
The 30th ordinary partial sum shows the beginnings of Gibbs phenomenon, the “bat ears” at the top of the square wave and their mirror image at the bottom. The 30th Cesàro partial sum is smoother and eliminates Gibbs phenomena near the discontinuity in the square wave.

What are the properties like for average of usual and cesaro summation in cases like the square wave?