Suppose you want to list the numbers from 0 to N in such a way that only one bit at a time changes between consecutive numbers. It’s not clear that this is even possible, but in fact it’s easy using Gray code, a method named after Frank Gray.
To convert an integer to its Gray code, take the XOR of the number with the number shifted right by 1.
def gray(n): return n ^ n >> 1
Here’s a little Python code to demonstrate this.
for i in range(8): print(format(gray(i), '03b'))
produces
000
001
011
010
110
111
101
100
Note that the numbers from 0 to 7 appear once, and each differs in exactly one bit from the numbers immediately above and below.
Let’s visualize the bits in Gray code with black squares for 1s and white squares for 0s.
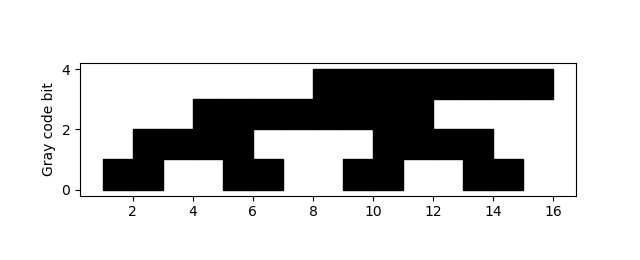
The code that produced the plot is very brief.
N = 4
M = 2**N
for i in range(N):
for j in range(M):
if gray(j) & 1<<i: # ith bit set
plt.fill_between([j, j+1], i, i+1, color="k")
plt.axes().set_aspect(1)
plt.ylabel("Gray code bit")
The bits are numbered from least significant to most significant, starting with 1.
If you want to see the sequence carried out further, increase N. If you do, you may want to comment out the line that sets the aspect ratio to be square because otherwise your plot will be much longer than tall.
Note that the Gray code of 2n − 1 is 2n−1, i.e. it only has one bit set. So if you were to wrap the sequence around, making a cylinder, you’d only change one bit at a time while going around the cylinder.
This could make a simple classroom activity. Students could reproduce the plot above by filling in squares on graph paper, then cut out the rectangle and tape the ends together.
See the next post for how to compute the inverse Gray code.

If one does not remember the equation for Gray code, it is quite easy to reconstruct (if you know that it exists) recursively, starting from trivial 1-bit code: take Grey code sequence for 2^{n-1}, reverse it, then extend original sequence with 0 most significant bit, and the reversed sequence with 1 in most significant bit position.
0
–
1
00
01
—
11
10
000
001
011
010
—
010
111
101
100
Here’s an example of a Gray code used in the physical world: a stadiometer in a pediatrician’s office.
Can I suggest replacing
plt.fill_between([j, j+1], i, i+1, color=”k”)
with
plt.fill_between([j, j+1], i-0.5, i+1-0.5, color=”k”)
The edges of the blocks in that figure fall right on the tick marks along the x-axis, making it hard to tell if a bit is set or not for a particular value. And if that isn’t ironic I don’t know what is.
My method for converting an integer to Gray code (bin) uses successive divisions by powers of 2 and looks at the parity of the rounded quotient. eg:
29/2=14.5~15 ➡ 1
29/4=7.3~7 ➡ 1
29/8=3.6~4 ➡ 0
29/16=1.8~2 ➡ 0
29/32=0.9~1 ➡ 1
The decimal value 29 has the binary value 10011 in Gray code.