The previous post mentioned a Math Overflow question about unexpected mathematical images, and reproduced one that looks like field grass. This post reproduces another set of images from that post.
Start anywhere in the complex plane with integer coordinates and walk west one unit at a time until you run into Gaussian prime [1]. Then turn left (counterclockwise) 90° and keep taking unit steps. Apparently this process will often (always?) return you to your starting point.
Different starting points lead to different patterns. Here’s an example given in the post, starting at 3 + 5i.
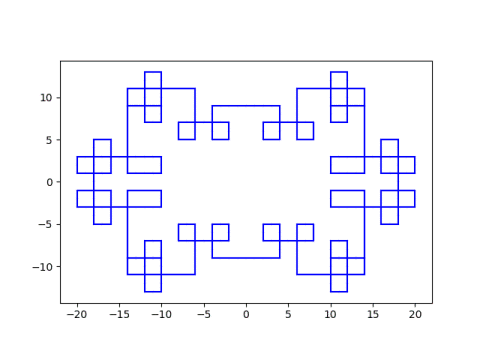
Here’s a more complex walk starting at 27 + 30i.
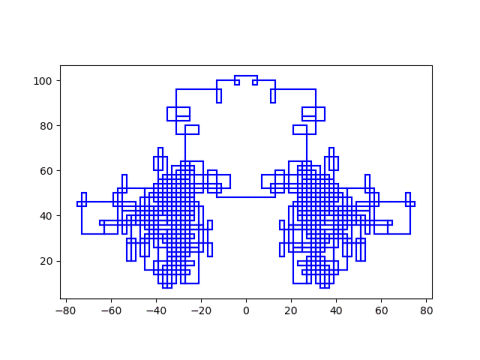
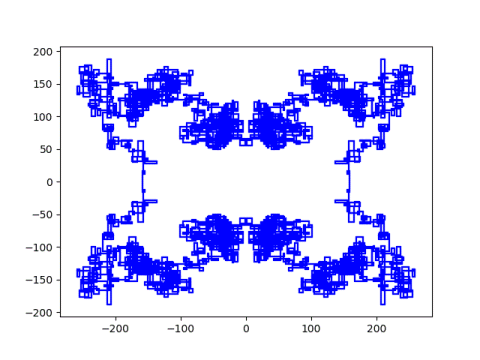
I tried starting at 127 + 131i and got a simple, uninteresting image. I tried again starting at 127 + 130i and got something much more complicated. I didn’t time it, but it took several minutes to plot.
Here’s the code that made the plots. (Note that Python uses j rather than i for imaginary unit.)
from sympy import isprime
import matplotlib.pyplot as plt
def isgaussprime(z: complex):
a, b = int(z.real), int(z.imag)
if a*b != 0:
return isprime(a**2 + b**2)
else:
c = abs(a+b)
return isprime(c) and c % 4 == 3
def connect(z1: complex, z2: complex):
plt.plot([z1.real, z2.real], [z1.imag, z2.imag], 'b')
start = 127 + 130j
#start = 3 + 5j
step = 1
z = start
next = None
while next != start:
next = z + step
connect(z, next)
if isgaussprime(next):
step *= 1j
z = next
plt.axes().set_aspect(1)
plt.show()
Related posts
[1] If a and b are integers, then a + bi is called a Gaussian integer. A Gaussian integer is a Gaussian prime if (1) both a and b are non-zero and a² + b² is prime, or (2) one of a or b is zero, and the absolute value of the non-zero part is a prime congruent to 3 mod 4.
Why is this definition so complicated? It’s actually a theorem. There’s a natural generalization of what it means to be prime in a commutative ring, and it works out that an element the Gaussian integers is prime if and only if the above criteria hold.
In general, a non-zero element p of a commutative ring R is prime if whenever p divides a product ab, p must either divide a or divide b.

I think your definition is missing the requirement that the element p needs to be a non-unit as well as non-zero.
It’s slightly faster if the line is only drawn at the Gaussian prime points.
Make these small changes:
last = z = start
remove the “connect(z, next)” line, and
if isgaussprime(next):
connect(last, next)
last = next
step *= 1j
I just tested all numbers from 0+0i to 500+500i.
It seems that the numbers of iterations are not equally distributed. Especially, I didn’t found any starting point with more than 3907940 iterations, but a surprisingly large number of starting points leads to this number of iterations, e.g. 206+321i.
Is this number (3907940) somehow special?
@Bernd: I haven’t looked at the code, but are a bunch of starting points on the same loop with 3907940 iterations? It’s such a big number it seems like it should include a significant fraction of the territory (and a lot of space outside the territory of starting points you’re including)