If you want to add ∞ to the real numbers, should you add one infinity or two? The answer depends on context. This post gives several examples each of when its appropriate to add one or two infinities.
Two infinities: relativistic addition
A couple days ago I wrote about relativistic addition, where the sum of two numbers x and y is defined by
where c is some positive constant. If we restrict x and y to be inside the open interval (-c, c) there are no complications. We could extend this to the closed interval [-c, c] with c acting like ∞ and –c acting like -∞. The addition rule above is based on addition of velocities in relativity, the speed of light acting like an infinity. There are two infinities, corresponding to light traveling in opposite directions. There is one caveat: c ⊕ (-c) is undefined.
One infinity: parallel addition
Another novel way to add real numbers is parallel addition.
This kind of addition comes up often in applications. For example, the combined resistance of two resistors in parallel is the parallel sum of their individual resistances, hence the name. The harmonic mean of two numbers is twice their parallel sum.
If we understand 1/∞ to be zero, then ∞ is the identity element for parallel addition, i.e.
Now there’s only one infinity. If we incorporated -∞ it would behave exactly like ∞.
Two infinities: IEEE numbers
Standard floating point numbers have two infinities; numbers can overflow in either the positive or negative direction. For more on that, see IEEE floating point exceptions and Anatomy of a floating point number.
One infinity: Posit numbers
Posit numbers are an alternative to IEEE floating point numbers. Unlike IEEE numbers, posit numbers have only one infinity. This is graphically depicted in the unum and posit project logo below.
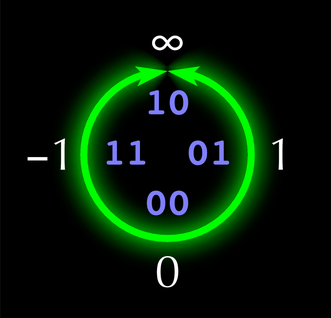
One advantage of posits for low-precision arithmetic because fewer bits are devoted to infinities and other exceptional numbers. The overhead of these non-numbers is relatively greater in low-precision.
For an introduction to posits, see Anatomy of a posit number.
Topology: compactification
Compactification is the process of adding points to a topological space in order to create a compact space. In topological terms, this post is about one-point compactification and two-point compactification.
The two-point compactification of the real numbers is the extended real numbers [-∞, ∞] which are homeomorphic (topologically equivalent) to a closed interval, like [0, 1].
The one-point compactification of the real numbers (-∞, ∞) ∪ ∞ is homeomorphic to a circle. Think of bending the real line into a circle with a point missing, then adding ∞ to fill in the missing point.
Parallel addition can be extended to the complex numbers, and there is still only need for one ∞ to make things complete. The one-point compactification of the complex plane is homeomorphic to a sphere.
Elliptic curves
Elliptic curves have a single point at infinity, and as with parallel addition the point at infinity is the additive identity. Interestingly, elliptic curves over finite fields have a finite number of points. That is, they have something that acts like infinity even though they do not have an infinite number of points. This shows that the algebraic and topological ideas of infinity are distinct from the idea of infinity as a cardinality.

I expected this to be about aleph null and aleph one, the cardinalities of the integers and reals. But the infinities here ended up being more interesting. Thank you!
I think the possibility of more than two points at infinity, as in projective spaces, also deserves a mention.