Broadcasting and functors

In my previous post, I looked at the map Δ that takes a column vector to a diagonal matrix. I even drew a commutative diagram, which foreshadows a little category theory.

Suppose you have a function f of a real or complex variable. To an R programmer, if x is a vector, it’s obvious that f(x) means to apply f to every component of a vector. Python (NumPy) works the same way, and calls this broadcasting. To a mathematician, this looks odd. What does the logarithm of a vector, for example, even mean?

As in the previous post, we can use Δ to formalize things. We said that Δ has some nice properties, and in fact we will show it is a functor.

To have a functor, we have to have categories. (Historically, functors came first; categories were defined in order to define functors.) We will define C to be the category of column vectors and M the category of square matrices as before. Or rather, we should say the objects of C are column vectors and the objects of M are square matrices.

Categories need morphisms, functions between objects [1]. We define the morphisms on C to be analytic functions applied componentwise. So, for example, if

z = [1, 2, −3],

then

tan(z) = [tan(1), tan(2), tan(−3)].

The morphisms on M will be analytic functions on square matrices, not applied componentwise but applied by power series. That is, given an analytic function f, we define f of a square matrix X as the result of sticking the matrix X into the power series for f. For an example, see What is the cosine of a matrix?

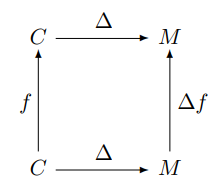
We said that Δ is a functor. It takes column vectors and turns them into square matrices by putting their contents along the diagonal of a matrix. We gave the example in the previous post that [4, i, π] would be mapped to the matrix with these elements on the diagonal, i.e.

That says what Δ does on objects, but what does it do on morphisms? It takes an analytic function that was applied componentwise to column vectors, and turns it into a function that is applied via its power series to square matrices. That is, starting with a function

we define the morphism f on C by

and the morphism Δ f on M by

where Z is a square matrix.

We can apply f to a column vector, and then apply Δ to turn the resulting vector into a diagonal matrix, or we could apply Δ to turn the vector into a diagonal matrix first, and then apply f (technically,  Δf). That is, the follow diagram commutes:

Python example

Applying an analytic function to a diagonal matrix gives the same result as simply applying the function to the elements of the diagonal. But for more general square matrices, this is not the case. We will illustrate this with some Python code.

    import numpy as np
    from scipy.linalg import funm

    d = np.array([1, 2])
    D = np.diag(d)
    M = np.array([[1, np.pi], [2, 0]])

Now let’s look at some output.

    >>> np.sin(d)                     
    array([0.84147098, 0.90929743])   

    >>> np.sin(D)                     
    array([[0.84147098, 0.        ],  
           [0.        , 0.90929743]]) 

    >>> funm(D, np.sin)               
    array([[0.84147098, 0.        ],  
           [0.        , 0.90929743]]) 

So if we take the sine of d and turn the result into a matrix, we get the same thing as if we turn d into a matrix D and then take the sine of D, either componentwise or as an analytic function (with funm, function of a matrix).

Now let’s look at a general, non-diagonal matrix.

    >>> np.sin(M)
    array([[0.84147099, 0],
       [0.90929743, 0]])

    >>> funm(D, np.sin)
    array([[0.84147098, 0.        ],
           [0.        , 0.90929743]])

Note that the elements in the bottom row are in opposite positions in the two examples.

[1] OK, morphisms are not necessarily functions, but in practice they usually are.