Moving between vectors and diagonal matrices

This is the first of two posts on moving between vectors and diagonal matrices. The next post is Broadcasting and functors.

Motivation

When I first saw the product of two vectors in R, I was confused. If x and y are vectors, what does x*y mean? An R programmer would say “You multiply components together, of course. What else could it mean?!”

But my first thought was “What kind of product do they mean? Inner product? Outer product? You can’t take the matrix product of two vectors.”

That was a long time ago. What brought this to mind today was a statistical paper I was reading that used the same symbol for a vector and a matrix. In context it wasn’t hard to figure out what the authors meant, but there was something implicit going on there that I will make explicit here.

Vectors and matrices

You can map a vector to a matrix by putting its contents along the diagonal of a diagonal matrix. That is, given a vector v of dimension n, create an n by n matrix V that is filled with zeros, except that

V_ii = v_i

for i = 1, 2, …, n. Let’s call this function Δ. In NumPy, Δ is implemented as the function diag. For example,

$\Delta: \begin{pmatrix} 4 \\ i \\ \pi \end{pmatrix} \mapsto \begin{pmatrix} 4 & 0 & 0\\ 0 & i & 0 \\ 0 & 0 & \pi \end{pmatrix}$

The statistics paper that I mentioned above used Δ implicitly, i.e. it denoted v and Δv with the same notation.

The function Δ has some nice properties.

The componentwise product two vectors is called the Hadamard product, denoted by a circle. You can first take the Hadamard product of two column vectors (of the same dimension) and then embed the result in a matrix using Δ, or you can first embed the two vectors into the world of matrices and take the product there. Either way you end up at the same place.

In other words, the following diagram commutes:

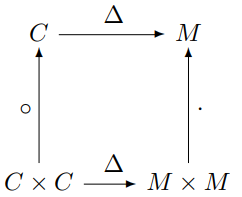
$\begin{diagram} C & \rTo^{\Delta} & M \\ \uTo^{\circ} & & \uTo_{\cdot} \\ C \times C & \rTo^{\Delta} & M \times M \end{diagram}$

Here C is the set of column vectors, and by C × C we mean pairs of column vectors of the same dimension. Similarly, M is the set of square matrices, and by M × M we mean pairs of square matrices of the same dimension. The circle on the left is Hadamard product. The dot on the right is ordinary matrix product [1].

The Δ on top is the Δ we’ve defined above. The Δ on bottom takes a pair of column vectors to a pair of matrices by operating on each element of the pair separately.

Although it would a little strange to do so, you could define Hadamard product this way. To take the Hadamard product of two vectors, take them over to the world of matrices, multiply the two matrices, and take that matrix back to the world of column vectors.

[1] Alternately, you could think of the product on the right as Hadamard product of matrices. For diagonal matrices, ordinary matrix product and Hadamard product coincide, though of course in general they are very different.

Motivation

Vectors and matrices

Related posts